题目内容
若函数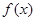 具有性质:①
具有性质:①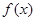 为偶函数,②对任意
为偶函数,②对任意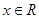 都有
都有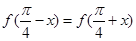 ,所以则函数
,所以则函数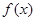 的解析式可以是:
的解析式可以是: (只需写出满足条件的一个解析式即可)
(只需写出满足条件的一个解析式即可)
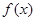 具有性质:①
具有性质:①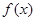 为偶函数,②对任意
为偶函数,②对任意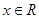 都有
都有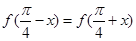 ,所以则函数
,所以则函数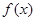 的解析式可以是:
的解析式可以是: (只需写出满足条件的一个解析式即可)
(只需写出满足条件的一个解析式即可)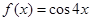
试题分析:由题意可知函数
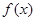 为偶函数而且
为偶函数而且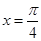 为函数的一条对称轴,
为函数的一条对称轴,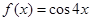 ,
,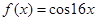 等都符合要求,写出一个即可.
等都符合要求,写出一个即可.点评:函数的奇偶性、单调性和周期性、对称性等是函数的重要的几何性质,要牢固掌握,灵活应用解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
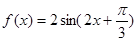 图象沿
图象沿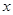 轴向左平移
轴向左平移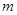 个单位(
个单位(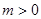 ),所得函数的图象关于
),所得函数的图象关于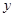 轴对称,则
轴对称,则



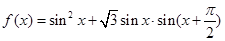 ,
,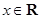
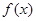 的最小正周期; (2)若
的最小正周期; (2)若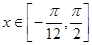 ,求函数
,求函数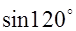 =( )
=( )



 -3cos
-3cos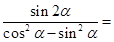 。
。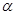 是钝角,则
是钝角,则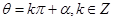 是( )
是( ) 等于( )
等于( )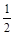

 ,
, ,则
,则 ( )
( ) 


