Question

【题目】椭圆 + =1的左焦点为F，直线x=a与椭圆相交于点M、N，当△FMN的周长最大时，△FMN的面积是（ ）
A.
B.
C.
D.

Answer 1

【答案】C
【解析】解：设右焦点为F′，连接MF′，NF′，∵|MF′|+|NF′|≥|MN|，

∴当直线x=a过右焦点时，△FMN的周长最大．

由椭圆的定义可得：△FMN的周长的最大值=4a=4 ．

c= =1．

把c=1代入椭圆标准方程可得： =1，解得y=± ．

∴此时△FMN的面积S= = ．

故选：C．

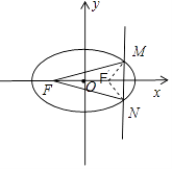
设右焦点为F′，连接MF′，NF′，由于|MF′|+|NF′|≥|MN|，可得当直线x=a过右焦点时，△FMN的周长最大．c= =1．把c=1代入椭圆标准方程可得： =1，解得y，即可得出此时△FMN的面积S．