题目内容
已知函数f(x)=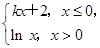 (k∈R),若函数y=|f(x)|+k有三个零点,则实数k的取值范围是( )
(k∈R),若函数y=|f(x)|+k有三个零点,则实数k的取值范围是( )
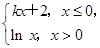 (k∈R),若函数y=|f(x)|+k有三个零点,则实数k的取值范围是( )
(k∈R),若函数y=|f(x)|+k有三个零点,则实数k的取值范围是( )| A.k≤2 | B.-1<k<0 | C.-2≤k<-1 | D.k≤-2 |
D
由y=|f(x)|+k=0得|f(x)|=-k≥0,所以k≤0,作出函数y=|f(x)|的图像,
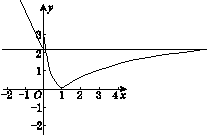
要使函数y=-k与y=|f(x)|的图像有三个交点,则有-k≥2,即k≤-2.

要使函数y=-k与y=|f(x)|的图像有三个交点,则有-k≥2,即k≤-2.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
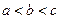 ,则函数
,则函数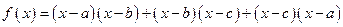 的两个零点分别位于区间( )
的两个零点分别位于区间( )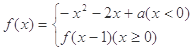 ,且函数
,且函数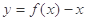 恰有3个不同的零点,则实数
恰有3个不同的零点,则实数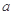 的取值范围是( )
的取值范围是( )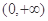
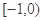
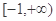

 在区间(k,k+1)(k∈N*)上存在零点,则k的值为________.
在区间(k,k+1)(k∈N*)上存在零点,则k的值为________.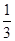 x-ln x(x>0),则y=f(x)( ).
x-ln x(x>0),则y=f(x)( ).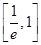 ,(1,e)内均有零点
,(1,e)内均有零点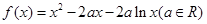 ,则下列说法不正确的是( )
,则下列说法不正确的是( )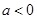 时,函数
时,函数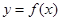 有零点
有零点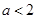
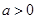 ,函数
,函数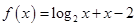 的零点在区间
的零点在区间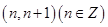 内,则
内,则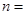 .
.