Question

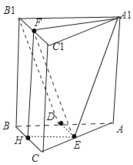
【题目】如图,已知直三棱柱中,,,,,点DE分别是边的中点,求:

(1)该直三棱柱的侧面积;

(2)异面直线与所成的角的大小(用反三角函数值表示)

Answer 1

【答案】(1);(2);

【解析】

(1)要求直三棱柱的侧面积,直三棱柱的高已经知道了,那么结合题意求出底面的三条棱长,进而可以计算出棱柱侧面积.

(2)通过构造平行四边形,将转化,使得的平行线与在同一平面内,然后计算出各边长度,最后运用余弦定理求出直线与所成的角的余弦值,进而求出结果.

(1)由题意知在三角形中, ,,,则,,又直三棱柱中,所以.综上直三棱柱的侧面积为.

(2)取的中点为,连接,,则,并且,因为点、分别是边的中点,所以,,所以,并且,所以四边形是平行四边形,所以,所以与异面直线与所成的角相等,取中点,连接、,因为,,点、分别是边的中点,所以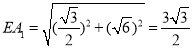,,,在三角形中,由余弦定理得,故.综上异面直线与所成的角的大小为.