题目内容
已知点P1(a1,b1),P2(a2,b2).…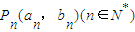 都在函数
都在函数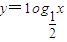 的图象上.
的图象上.(1)若数列{bn}是等差数列,求证数列{an}是等比数列;
(2)若数列{an}的前n项和是
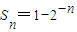 ,过点Pn,Pn+1的值线与两坐标轴所围三角形面积为cn,求最小的实数t使cn≤t对n∈N*恒成立;
,过点Pn,Pn+1的值线与两坐标轴所围三角形面积为cn,求最小的实数t使cn≤t对n∈N*恒成立;(3)若数列{bn}为由(2)中{an}得到的数列,在bk与bk+1之间插入3k-1(k∈N*)个3,得一新数列{dn},问是否存在这样的正整数m,使数列{dn}的前m项的和Sm=2008,如果存在,求出m的值,如果不存在,请说明理由.
【答案】分析:(1)利用数列{bn}是等差数列,结合等比数列的定义,即可证明数列{an}是等比数列;
(2)先确定数列{an}的通项公式,再求数列{bn}的通项公式,进而可得直线方程,由此可求数列{cn}的通项,利用各项依次单调递减,可求最小的实数t;
(3)求出数列{dn}中,bk(含bk项)前的所有项的和,由此可求m的值.
解答:(1)证明:数列{bn}是等差数列,设公差为d,则bn+1-bn=d对n∈N*恒成立,…(1分)
依题意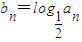 ,
,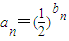 ,…(2分)
,…(2分)
所以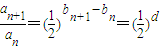 是定值,…(3分)
是定值,…(3分)
从而数列{an}是等比数列. …(4分)
(2)解:当n=1时,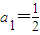 ,当n≥2时,
,当n≥2时,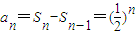 ,n=1也适合此式,
,n=1也适合此式,
即数列{an}的通项公式是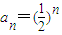 . …(5分)
. …(5分)
由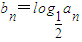 ,可得数列{bn}的通项公式是bn=n,…(6分)
,可得数列{bn}的通项公式是bn=n,…(6分)
所以 ,
,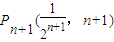 .
.
过这两点的直线方程是: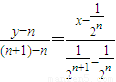 ,可得与坐标轴的交点是
,可得与坐标轴的交点是 和Bn(0,n+2).…(7分)
和Bn(0,n+2).…(7分)
∴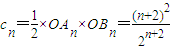 ,…(8分)
,…(8分)
由于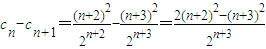 =
=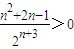 …(9分)
…(9分)
即数列{cn}的各项依次单调递减,所以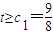 . …(10分)
. …(10分)
(3)解:数列{dn}中,bk(含bk项)前的所有项的和是(1+2+…+k)+(31+32+…+3k-1)=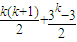 …(11分)
…(11分)
当k=7时,其和是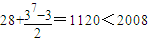 ,…(12分)
,…(12分)
当k=8时,其和是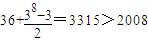 ,
,
又因为2008-1120=888=296×3,是3的倍数,故存在这样的m,使得Sm=2008,…(13分)
此时m=7+(1+3+32+…+35)+296=667. …(14分)
点评:本小题主要考查等差、等比数列的定义、通项、求和、对数的运算、直线方程与不等式等知识,考查化归、转化、方程的数学思想方法,以及抽象概括能力、运算求解能力、创新能力和综合应用能力.
(2)先确定数列{an}的通项公式,再求数列{bn}的通项公式,进而可得直线方程,由此可求数列{cn}的通项,利用各项依次单调递减,可求最小的实数t;
(3)求出数列{dn}中,bk(含bk项)前的所有项的和,由此可求m的值.
解答:(1)证明:数列{bn}是等差数列,设公差为d,则bn+1-bn=d对n∈N*恒成立,…(1分)
依题意
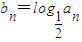 ,
,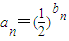 ,…(2分)
,…(2分)所以
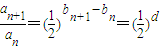 是定值,…(3分)
是定值,…(3分)从而数列{an}是等比数列. …(4分)
(2)解:当n=1时,
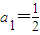 ,当n≥2时,
,当n≥2时,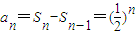 ,n=1也适合此式,
,n=1也适合此式,即数列{an}的通项公式是
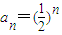 . …(5分)
. …(5分)由
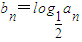 ,可得数列{bn}的通项公式是bn=n,…(6分)
,可得数列{bn}的通项公式是bn=n,…(6分)所以
 ,
,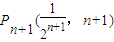 .
.过这两点的直线方程是:
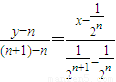 ,可得与坐标轴的交点是
,可得与坐标轴的交点是 和Bn(0,n+2).…(7分)
和Bn(0,n+2).…(7分)∴
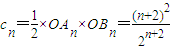 ,…(8分)
,…(8分)由于
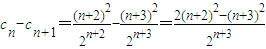 =
=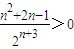 …(9分)
…(9分)即数列{cn}的各项依次单调递减,所以
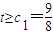 . …(10分)
. …(10分)(3)解:数列{dn}中,bk(含bk项)前的所有项的和是(1+2+…+k)+(31+32+…+3k-1)=
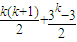 …(11分)
…(11分)当k=7时,其和是
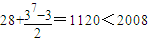 ,…(12分)
,…(12分)当k=8时,其和是
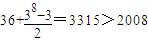 ,
,又因为2008-1120=888=296×3,是3的倍数,故存在这样的m,使得Sm=2008,…(13分)
此时m=7+(1+3+32+…+35)+296=667. …(14分)
点评:本小题主要考查等差、等比数列的定义、通项、求和、对数的运算、直线方程与不等式等知识,考查化归、转化、方程的数学思想方法,以及抽象概括能力、运算求解能力、创新能力和综合应用能力.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 ,其中{an}、{bn}分别为等差数列和等比数列,O为坐标原点,若P1是线段AB的中点.
,其中{an}、{bn}分别为等差数列和等比数列,O为坐标原点,若P1是线段AB的中点.