题目内容
【题目】通过市场调查,得到某种产品的资金投入![]() (单位:万元)与获得的利润
(单位:万元)与获得的利润![]() (单位:千元)的数据,如表所示
(单位:千元)的数据,如表所示
资金投入 | 2 | 3 | 4 | 5 |
利润 | 2 | 3 | 5 | 6 |
(1)根据上表提供的数据,用最小二乘法求线性回归直线方程![]() ;
;
(2)该产品的资金投入每增加![]() 万元,获得利润预计可增加多少千元?若投入资金
万元,获得利润预计可增加多少千元?若投入资金![]() 万元,则获得利润的估计值为多少千元?
万元,则获得利润的估计值为多少千元?
参考公式: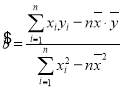
【答案】(1)![]() (2)获得利润预计增加
(2)获得利润预计增加![]() 千元,获得利润的估计值为
千元,获得利润的估计值为![]() 千元
千元
【解析】
(1)利用公式求出![]() ,再将样本中心点代入求出
,再将样本中心点代入求出![]() 即可求解.
即可求解.
(2)将![]() 代入(1)中的回归直线方程即可求解.
代入(1)中的回归直线方程即可求解.
解:(1)![]()
![]()
![]()
![]()
∴![]() ,
,
![]() .
.
∴线性回归方程为![]() .
.
(2)由(1)可知,资金投入每增加![]() 万元,获得利润预计增加
万元,获得利润预计增加![]() 千元
千元
当![]() 时,
时,![]() (千元),
(千元),
∴当投入资金![]() 万元,获得利润的估计值为
万元,获得利润的估计值为![]() 千元
千元

练习册系列答案
相关题目
【题目】某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价![]() 和月销售量
和月销售量![]() 之间的一组数据,如下表所示:
之间的一组数据,如下表所示:
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(1)根据统计数据,求出![]() 关于
关于![]() 的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
(2)生产企业与网店约定:若该新产品的月销售量不低于10万件,则生产企业奖励网店1万元;若月销售量不低于8万件且不足10万件,则生产企业奖励网店5000元;若月销售量低于8万件,则没有奖励.现用样本估计总体,从上述5个销售单价中任选2个销售单价,下个月分别在两个不同的网店进行销售,求这两个网店下个月获得奖励的总额![]() 的分布列及其数学期望.
的分布列及其数学期望.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为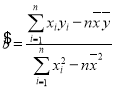 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.