题目内容
(本小题满分13分)设数列 的前
的前 项和为
项和为 .已知
.已知 ,
, ,
, .
.
(1)写出 的值,并求数列
的值,并求数列 的通项公式;
的通项公式;
(2)记 为数列
为数列 的前
的前 项和,求
项和,求 ;
;
(3)若数列 满足
满足 ,
, ,求数列
,求数列 的通项公式.
的通项公式.
(1) ;(2)
;(2) ;(3)
;(3)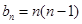 。
。
解析试题分析:(Ⅰ)由已知得, ,
, . …………………2分
. …………………2分
由题意, ,则当
,则当 时,
时, .
.
两式相减,得 (
( ). ………………………3分
). ………………………3分
又因为 ,
, ,
, ,
,
所以数列 是以首项为
是以首项为 ,公比为
,公比为 的等比数列,
的等比数列,
所以数列 的通项公式是
的通项公式是 (
( ). ………………………………4分
). ………………………………4分
(Ⅱ)因为 ,
,
所以 , ……………………5分
, ……………………5分
两式相减得, , ………7分
, ………7分
整理得, (
( ). ………………………………8分
). ………………………………8分
(Ⅲ) 当 时,依题意得
时,依题意得 ,
, ,… ,
,… ,  .
.
相加得, . …………………11分
. …………………11分
依题意 .
.
因为 ,所以
,所以 (
( ).
).
显然当 时,符合.
时,符合.
所以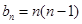 (
( ). …………………13分
). …………………13分
考点:数列通项公式的求法。错位相减法求数列前n项和。
点评:我们要熟练掌握求数列通项公式的方法。公式法是求数列通项公式的基本方法之一,常用的公式有:等差数列的通项公式、等比数列的通项公式及公式 。此题的第一问求数列的通项公式就是用公式
。此题的第一问求数列的通项公式就是用公式 ,用此公式要注意讨论
,用此公式要注意讨论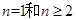 的情况。
的情况。

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
 :
: 上的点
上的点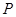 到点
到点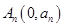 的距离的最小值为
的距离的最小值为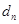 ,若
,若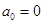 ,
,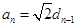 ,
,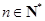
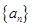 的通项公式;
的通项公式; ;
;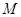 ,使得对
,使得对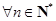 ,都有不等式:
,都有不等式: 成立?请说明理由.
成立?请说明理由.  的前n项和
的前n项和 ,且
,且 是
是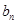 与1的等差中项。
与1的等差中项。 的通项公式;
的通项公式; ,求
,求
 ,是否存在
,是否存在 ,使得
,使得 并说明理由。
并说明理由。 为单调递增的等差数列,
为单调递增的等差数列, ,且
,且 依次成等比数列.
依次成等比数列. ;
; ,求数列
,求数列 的前
的前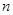 项和
项和 ;
; ,求数列
,求数列 的前
的前 .
.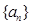 的前
的前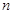 项和为
项和为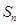 ,公差d
,公差d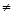 0,
0,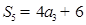 ,且
,且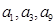 成等比数列.
成等比数列.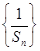 的前
的前 中,
中, ,
, (
( )
) ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证:  .
.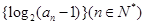 为等差数列,且
为等差数列,且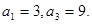
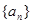 的通项公式;
的通项公式;
 的前n项和为
的前n项和为 ,且满足
,且满足 ,
, ,
, ,数列
,数列 为等比数列,求实数
为等比数列,求实数 的值;
的值; ,求数列
,求数列 的通项公式;
的通项公式; ,求数列
,求数列 的前n项和
的前n项和 .
.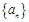 满足条件:
满足条件: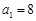 ,
,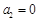 ,
,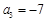 ,且数列
,且数列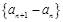
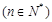 是等差数列.
是等差数列.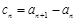 ,求数列
,求数列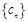 的通项公式;
的通项公式;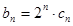 , 求
, 求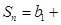
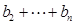 ;
;