题目内容
(本题满分12分)设函数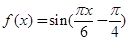 +2
+2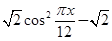 。
。
(1)求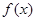 的最小正周期。
的最小正周期。
(2)若函数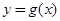 与
与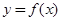 的图象关于直线
的图象关于直线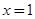 对称,当
对称,当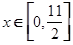 时,求函数
时,求函数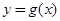 的最小值与相应的自变量
的最小值与相应的自变量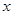 的值。
的值。
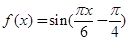 +2
+2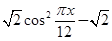 。
。(1)求
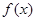 的最小正周期。
的最小正周期。(2)若函数
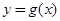 与
与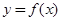 的图象关于直线
的图象关于直线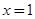 对称,当
对称,当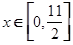 时,求函数
时,求函数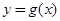 的最小值与相应的自变量
的最小值与相应的自变量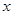 的值。
的值。解:(1)
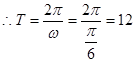
(2)
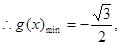 此时
此时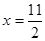 。
。本试题主要是考查了三角函数的周期公式和三角函数的图像与性质的综合运用。
(1)先利用二倍角公式化简关系式,化为单一三角函数,然后利用正弦的周期公式求解得到。
(2)根据里那个图像关于直线x=1对称可知在对称区间上,函数的最值。
解:(1)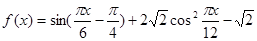
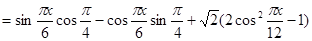 ----------(1分)
----------(1分)
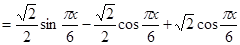 ---------------------(3分)
---------------------(3分)
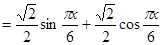 --------------------------------(4分)
--------------------------------(4分)
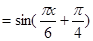 ------------------------------------------(5分)
------------------------------------------(5分)
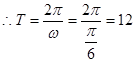 ----------------------------------------(6分)
----------------------------------------(6分)
(2)方法一:由题意知道:
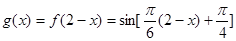 -------------------------------------(8分)
-------------------------------------(8分)
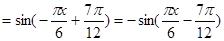 ------------------------(9分)
------------------------(9分)
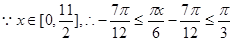 ----------------------------------(10分)
----------------------------------(10分)
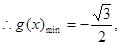 此时
此时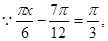 即
即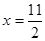 ----------------------(12分)
----------------------(12分)
方法二:可以根据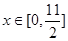 关于
关于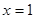 的对称区间
的对称区间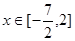 上函数
上函数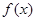 的最值。
的最值。
(1)先利用二倍角公式化简关系式,化为单一三角函数,然后利用正弦的周期公式求解得到。
(2)根据里那个图像关于直线x=1对称可知在对称区间上,函数的最值。
解:(1)
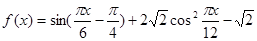
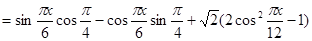 ----------(1分)
----------(1分)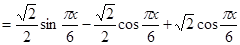 ---------------------(3分)
---------------------(3分)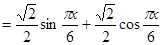 --------------------------------(4分)
--------------------------------(4分)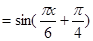 ------------------------------------------(5分)
------------------------------------------(5分)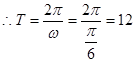 ----------------------------------------(6分)
----------------------------------------(6分)(2)方法一:由题意知道:
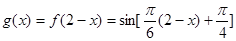 -------------------------------------(8分)
-------------------------------------(8分)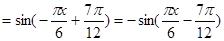 ------------------------(9分)
------------------------(9分)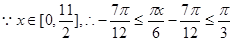 ----------------------------------(10分)
----------------------------------(10分)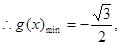 此时
此时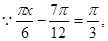 即
即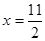 ----------------------(12分)
----------------------(12分)方法二:可以根据
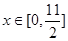 关于
关于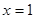 的对称区间
的对称区间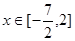 上函数
上函数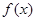 的最值。
的最值。
练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
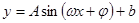 (如图所示,单位:摄氏温度,
(如图所示,单位:摄氏温度,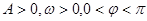 ).
).
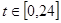 ,单位小时)
,单位小时)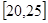 时的时间.
时的时间.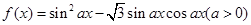 的图象与直线
的图象与直线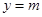 相切,相邻切点之
相切,相邻切点之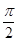 。
。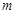 和
和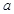 的值;
的值;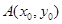 是
是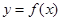 图象的对称中心,且
图象的对称中心,且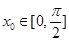 ,求点
,求点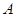 的坐标。
的坐标。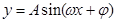 在一个周期内的图象,此函数的解析式为可为( )
在一个周期内的图象,此函数的解析式为可为( )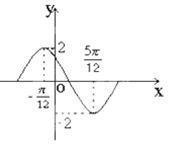
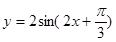
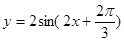
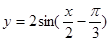
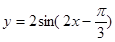
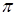 ,且图象关于直线
,且图象关于直线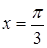 对称的函数是
对称的函数是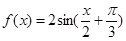

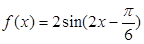
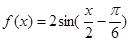
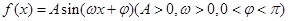 ,其导函数
,其导函数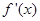 的部分图像如图所示,则函数
的部分图像如图所示,则函数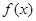 的解析式为( )
的解析式为( )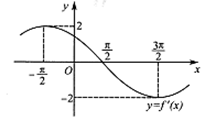




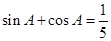
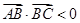
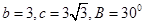
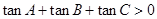
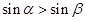 ,则下列命题中,正确的是
,则下列命题中,正确的是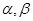 为第一象限角,则
为第一象限角,则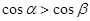
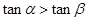
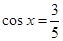 ,
, ,则
,则 .
.