题目内容
向量
与向量
=(-3,4)的夹角为π,|
|=10,若点A的坐标是(1,2),则点B的坐标为( )
| AB |
| a |
| AB |
分析:向量
与向量
夹角为π,可设
=(-3k,4k),其中k<0.由向量模的公式列式可解出k=-2,从而得到
=(6,-8).再根据向量
的起点A的坐标(1,2),可得向量
的终点B的坐标.
| AB |
| a |
| AB |
| AB |
| AB |
| AB |
解答:解:∵向量
与向量
=(-3,4)的夹角为π,
∴设
=k
=k(-3,4)=(-3k,4k),其中k<0
由此可得|
|=
=10,解之得k=-2(舍2)
∴
=(6,-8)
由点A的坐标是(1,2),设B(m,n),
得
=(m-1,n-2)=(6,-8)
则有
,解之得m=7,n=-6
∴点B的坐标为(7,-6),
故选:D
| AB |
| a |
∴设
| AB |
| a |
由此可得|
| AB |
| (-3k)2+(4k)2 |
∴
| AB |
由点A的坐标是(1,2),设B(m,n),
得
| AB |
则有
|
∴点B的坐标为(7,-6),
故选:D
点评:本题给出一个向量的模的大小,且和已知向量反向的情况下求向量的坐标,着重考查了平面向量的坐标运算和向量模的公式等知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,
?
∈[
,
],其面积S=
,则向量
与向量
夹角的取值范围是( )
| AB |
| BC |
| 3 |
| 8 |
3
| ||
| 8 |
| 3 |
| 16 |
| AB |
| BC |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
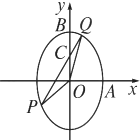 已知椭圆
已知椭圆