Question

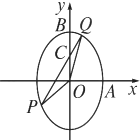已知椭圆

y2

a2

+

x2

b2

=1的一个焦点为F(0，2

2

)，与两坐标轴正半轴分别交于A，B两点（如图），向量

AB

与向量

m

=(-1，

2

)共线．
（1）求椭圆的方程；
（2）若斜率为k的直线过点C（0，2），且与椭圆交于P，Q两点，求△POC与△QOC面积之比的取值范围．

Answer 1

分析：（1）利用向量共线，确定a，b的关系，结合椭圆的焦点坐标，即可求得椭圆的方程；
（2）直线方程代入椭圆方程，利用韦达定理，即可求得比值的范围．

解答：解：（1）由向量

AB

与向量

m

=(-1，

2

)共线，可得

a

b

=

2

∵焦点为F(0，2

2

)，∴a²-b²=8，∴b²=8，a²=16
∴椭圆的方程为

y2

16

+

x2

8

=1；
（2）设P（x₁，y₁），Q（x₂，y₂），且x₁＜0，x₂＞0，
PQ的方程为y=kx+2，代入椭圆方程消去y，可得（2+k²）x²+4kx-12=0
∴x₁+x₂=-

4k

2+k2

①，x₁x₂=-

12

2+k2

②
设△POC与△QOC面积之比为λ，即-

x2

x1

=λ
结合①②得（1-λ）x₁=-

4k

2+k2

，λx₁²=-

12

2+k2

∴

λ

(1-λ)2

=

3

4

(1+

2

k2

)＞

3

4

∴

1

3

＜λ＜3
∴△POC与△QOC面积之比的取值范围为

1

3

＜λ＜3．

点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查向量知识的运用，正确运用韦达定理是关键．