题目内容
A、B两篮球队进行比赛,规定若一队胜4场则此队获胜且比赛结束(七局四胜制),A、B两队在每场比赛中获胜的概率均为
,ξ为比赛需要的场数,则Eξ=( )
| 1 |
| 2 |
分析:先确定比赛需要的场数ξ的取值,求出相应的概率,即可求得数学期望.
解答:解:由题设知,比赛需要的场数ξ为4,5,6,7.
p(ξ=4)=(
)4+(
)4=
;p(ξ=5)=2×
×(
)3×
×
=
;p(ξ=6)=2
×(
)3×(
)2×
=
p(ξ=7)=2
×(
)3×(
)3×
=
∴Eξ=4×
+5×
+6×
+7×
=
故选B.
p(ξ=4)=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| C | 3 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| C | 3 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 16 |
p(ξ=7)=2
| C | 3 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 16 |
∴Eξ=4×
| 1 |
| 8 |
| 1 |
| 4 |
| 5 |
| 16 |
| 5 |
| 16 |
| 93 |
| 16 |
故选B.
点评:本题考查离散型随机变量的数学期望,考查学生的运算能力,确定变量的取值,求出相应的概率是关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 ,ξ为比赛需要的场数,则Eξ=( )
,ξ为比赛需要的场数,则Eξ=( )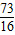
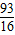
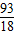
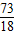
 ,ξ为比赛需要的场数,则Eξ= .
,ξ为比赛需要的场数,则Eξ= .