题目内容

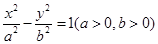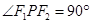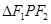已知F1、F2分别是双曲线的左、右焦点，P为双曲线上的一点，若，且的三边长成等差数列，则双曲线的离心率是        .

 

【答案】

5   

【解析】

试题分析：设|PF1|=m，|PF2|=n，不妨设P在第一象限，则由已知得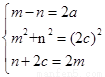 ，∴5a2-6ac+c2=0，方程两边同除a2得：即e2-6e+5=0，解得e=5或e=1（舍去），故答案为5．

考点：本题考查了双曲线的性质

点评：解题过程中，为了解答过程的简便，我们把未知|PF1|设为m，|PF2|设为n，这时要求离心率e，我们要找出a，c之间的关系，则至少需要三个方程，由已知中，若∠F1PF2=90°，且△F1PF2的三边长成等差数列，我们不难得到两个方程，此时一定要注意双曲线的定义，即P点到两个焦点的距离之差为定值．

 

练习册系列答案
相关题目
（2013•湖南）已知F1，F2分别是椭圆E：
x25
+y2=1的左、右焦点F1，F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点．
（Ⅰ）求圆C的方程；
（Ⅱ）设过点F2的直线l被椭圆E和圆C所截得的弦长分别为a，b．当ab最大时，求直线l的方程．
（2013•青岛二模）已知F1、F2分别是双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右焦点，P为双曲线右支上的一点，
PF2
⊥
F1F2
，且|
PF1
|=
2
|
PF2
|，则双曲线的离心率为（　　）
已知F1，F2分别是双曲线
x2
a2
-
y2
b2
=1 (a＞0， b＞0)的左、右焦点，过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M，若点M在以线段F1F2为直径的圆外，则双曲线离心率的取值范围是（　　）
如图，已知F1，F2分别是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，且椭圆C的离心率e=
1
2
，F1也是抛物线C1：y2=-4x的焦点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点F2的直线l交椭圆C于D，E两点，且2
DF2
=
F2E
，点E关于x轴的对称点为G，求直线GD的方程．
已知F1，F2分别是双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)的左，右焦点，P是双曲线的上一点，若
PF1
•
PF2
=0且|
PF1
|•|
PF2
|=3ab，则双曲线的离心率是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网