题目内容
15.定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界,已知函数f(x)=4x-a•2x(1)a=2时.求函数f(x)的值域;
(2)求函数f(x)在x∈[0,1]的最小值g(a);
(3)若函数f(x)在x∈(-∞,0]上是以1为上界的有界函数.求实数a的取值范围.
分析 (1)当a=2时,令t=2x(t>0),则f(x)=g(t)=t2-2t,配方,即可得到所求值域;
(2)令t=2x,由0≤x≤1,可得1≤t≤2,函数y=t2-at=(t-$\frac{a}{2}$)2-$\frac{{a}^{2}}{4}$,对称轴为t=$\frac{a}{2}$,讨论对称轴和区[1,2]的关系,结合单调性,即可得到所求最小值;
(3)由题意知,|f(x)|≤1在(-∞,0]上恒成立,即2x-2-x≤a≤2-x+2x在(-∞,0]上恒成立.由指数函数的单调性和恒成立思想,求得最值,即可得到所求范围.
解答 解:(1)当a=2时,f(x)=4x-2•2x,
令t=2x(t>0),
则f(x)=g(t)=t2-2t=(t-1)2-1.
由t>0可得t=1时,取得最小值-1,无最大值,
即f(x)的值域为[-1,+∞);
(2)令t=2x,由0≤x≤1,可得1≤t≤2,
函数y=t2-at=(t-$\frac{a}{2}$)2-$\frac{{a}^{2}}{4}$,对称轴为t=$\frac{a}{2}$,
当$\frac{a}{2}$≤1即a≤2时,[1,2]为增区间,
即有最小值为g(a)=1-a;
当1<$\frac{a}{2}$<2时,即2<a<4时,最小值为g(a)=-$\frac{{a}^{2}}{4}$;
当$\frac{a}{2}$≥2即a≥4时,[1,2]为减区间,
即有最小值为g(a)=4-2a.
综上可得,g(a)=$\left\{\begin{array}{l}{1-a,a≤2}\\{-\frac{{a}^{2}}{4},2<a<4}\\{4-2a,a≥4}\end{array}\right.$;
(3)由题意知,|f(x)|≤1在(-∞,0]上恒成立.
∴-1≤f(x)≤1,即为-(2x+2-x)≤-a≤2-x-2x,
即2x-2-x≤a≤2-x+2x在(-∞,0]上恒成立.
由x≤0,可得2x∈(0,1],
即有2-x+2x∈[2,+∞),2x-2-x∈(-∞,0],
即有0≤a≤2,
故实数a的取值范围是[0,2].
点评 本题主要考查可化为二次函数在闭区间上的最值,利用函数的单调性求函数的最值,函数的恒成立问题,属于中档题.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案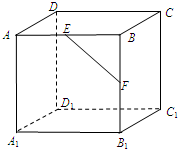 如图,正方体ABCD-A1B1C1D1中E,F分别是棱AB,BB1的中点,则异面直线DD1和EF所成的角的大小为45°.
如图,正方体ABCD-A1B1C1D1中E,F分别是棱AB,BB1的中点,则异面直线DD1和EF所成的角的大小为45°.