题目内容
19. 如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD.(Ⅰ)证明:C1C⊥BD;
(Ⅱ)当![]() 的值为多少时,能使A1C⊥平面C1BD?请给出证明.
的值为多少时,能使A1C⊥平面C1BD?请给出证明.
19.本小题主要考查直线与直线、直线与平面的关系,逻辑推理能力.
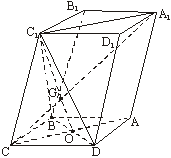
(Ⅰ)证明:连结A1C1、AC,AC和BD交于O,连结C1O.
∵四边形ABCD是菱形,∴AC⊥BD,BC=CD.
又∵∠BCC1=∠DCC1,C1C=C1C,∴△C1BC≌△C1DC,
∴C1B=C1D.∵DO=OB,∴C1O⊥BD,
但 AC⊥BD,AC∩C1O=O,∴BD⊥平面AC1.
又 C1C![]() 平面AC1,∴C1C⊥BD.
平面AC1,∴C1C⊥BD.
(Ⅱ)当![]() =1时,能使A1C⊥平面C1BD.
=1时,能使A1C⊥平面C1BD.
证明一:∵![]() =1,∴BC=CD=C1C,
=1,∴BC=CD=C1C,
又 ∠BCD=∠C1CB=∠C1CD.
由此可推得 BD=C1B=C1D.
∴三棱锥C-C1BD是正三棱锥.
设 A1C与C1O相交于G.
∵A1C1∥AC,且A1C1∶OC=2∶1,
∴C1G∶GO=2∶1.
又 C1O是正三角形C1BD的BD边上的高和中线,
∴点G是正三角形C1BD的中心,∴CG⊥平面C1BD.
即 A1C⊥平面C1BD.
证明二:由(Ⅰ)知,BD⊥平面AC1,
∵A1C![]() 平面AC1,
平面AC1,
∴BD⊥A1C.
当![]() =1时,平行六面体的六个面是全等的菱形,
=1时,平行六面体的六个面是全等的菱形,
同BD⊥A1C的证法可得BC1⊥A1C.
又 BD∩BC1=B,
∴A1C⊥平面C1BD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且
如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱)
如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱) 如图,已知平行六面体ABCD-A1B1C1D1.
如图,已知平行六面体ABCD-A1B1C1D1.