题目内容
设函数f(x)=x2+2lnx,用f′(x)表示f(x)的导函数, ,其中m∈R,且m>0.
,其中m∈R,且m>0.
(1)求函数f(x)的单调区间;
(2)若对任意的x1、 都有f′(x1)≤g′(x2)成立,求m实数的取值范围;
都有f′(x1)≤g′(x2)成立,求m实数的取值范围;
(3)试证明:对任意正数a和正整数n,不等式[f′(a)]n-2n-1f′(an)≥2n(2n-2).
解:(1)f(x)的定义域为(0,+∞)
f′(x)=2x+
∴f′(x)>0在(0,+∞)恒成立
故f(x)的单调递增区间为(0,+∞),无单调递减区间.
(2)据题意,问题转化为f′(x)最大值≤g′(x)的最小值
令∅(x)=f′(x)
∵
当 时,∅′(x)<0
时,∅′(x)<0
∴ 为减函数
为减函数
∴∅(x)在 的最大值为
的最大值为
∵ =
= =
=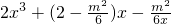
∴
令t=6x2则h(t)= 由
由 知
知 转化为求函数h(t)=
转化为求函数h(t)= 在
在 上最小值
上最小值

 (当且仅当t=m时取等号)
(当且仅当t=m时取等号)
①若 时,g′(x)的最小值为h(m)=
时,g′(x)的最小值为h(m)=
此时由f′(x)最大值≤g′(x)的最小值得 解得
解得
∴
②若m>6时,函数y=h(t)在[ 上为减函数
上为减函数
即g′(x)的最小值为h(6) 由题意有
由题意有 恒成立
恒成立
∴m>6
③若 时,函数y=h(t)在
时,函数y=h(t)在 为增函数,则g′(x)的最小值为
为增函数,则g′(x)的最小值为
因此,必须 此时无解
此时无解
综上所述,m实数的取值范围
(III)问题即证
即证
下面用数学归纳法证明
当n=1时,左边=0,右边=0不等式成立
假设n=k(k≥1)时成立即
则当n=k+1时,
 ≥(2k-2)×2+2=2k+1-2
≥(2k-2)×2+2=2k+1-2
即当n=k+1时原不等式成立
分析:(1)牵扯出函数的定义域,求出导函数,判断出导函数在定义域上大于0恒成立,得到函数在定义域上单调递增.
(2)先将问题转化为“f′(x)最大值≤g′(x)的最小值”,利用导函数求出f′(x)的最大值,再利用导数
求g′(x)的最小值需度m的范围分类讨论,求出最小值,列出不等式,求出m的范围.
(3)求出各个导数值,用分析法将要证的不等式化简,利用数学归纳法分三步得证.
点评:求不等式恒成立问题的一般思路是分离参数,构造新函数,求函数的最值,有时也直接将问题转化为求两个函数的最值;求函数的最值常利用导数研究函数的单调性求出,但若函数中有参数,一般要注意讨论.
f′(x)=2x+

∴f′(x)>0在(0,+∞)恒成立
故f(x)的单调递增区间为(0,+∞),无单调递减区间.
(2)据题意,问题转化为f′(x)最大值≤g′(x)的最小值
令∅(x)=f′(x)
∵

当
 时,∅′(x)<0
时,∅′(x)<0∴
 为减函数
为减函数∴∅(x)在
 的最大值为
的最大值为
∵
 =
= =
=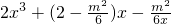
∴

令t=6x2则h(t)=
 由
由 知
知 转化为求函数h(t)=
转化为求函数h(t)= 在
在 上最小值
上最小值
 (当且仅当t=m时取等号)
(当且仅当t=m时取等号)①若
 时,g′(x)的最小值为h(m)=
时,g′(x)的最小值为h(m)=
此时由f′(x)最大值≤g′(x)的最小值得
 解得
解得
∴

②若m>6时,函数y=h(t)在[
 上为减函数
上为减函数即g′(x)的最小值为h(6)
 由题意有
由题意有 恒成立
恒成立∴m>6
③若
 时,函数y=h(t)在
时,函数y=h(t)在 为增函数,则g′(x)的最小值为
为增函数,则g′(x)的最小值为
因此,必须
 此时无解
此时无解综上所述,m实数的取值范围

(III)问题即证

即证

下面用数学归纳法证明
当n=1时,左边=0,右边=0不等式成立
假设n=k(k≥1)时成立即

则当n=k+1时,

 ≥(2k-2)×2+2=2k+1-2
≥(2k-2)×2+2=2k+1-2即当n=k+1时原不等式成立
分析:(1)牵扯出函数的定义域,求出导函数,判断出导函数在定义域上大于0恒成立,得到函数在定义域上单调递增.
(2)先将问题转化为“f′(x)最大值≤g′(x)的最小值”,利用导函数求出f′(x)的最大值,再利用导数
求g′(x)的最小值需度m的范围分类讨论,求出最小值,列出不等式,求出m的范围.
(3)求出各个导数值,用分析法将要证的不等式化简,利用数学归纳法分三步得证.
点评:求不等式恒成立问题的一般思路是分离参数,构造新函数,求函数的最值,有时也直接将问题转化为求两个函数的最值;求函数的最值常利用导数研究函数的单调性求出,但若函数中有参数,一般要注意讨论.

练习册系列答案
相关题目