Question

8．已知点椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离小率为$\frac{1}{2}$，F（1，0）为椭圆的一个焦点．
（I）求椭圆C的方程；
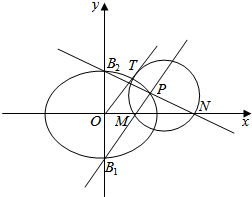
（Ⅱ）如图，设B₁B₂是椭圆C的短轴上的下顶点和上顶点，P是椭圆上异于B₁B₂的一点，直线B₁P与x轴交M，直线B₂P与x轴交于点N，又OT是由原点做出的经过M，N两点的圆的切线，T为切点，求|OT|的长．

Answer 1

分析 （I）由题意可得：$\left\{\begin{array}{l}{\frac{c}{a}=\frac{1}{2}}\\{c=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$，解出即可得出；
（II）设P$（2sinθ，\sqrt{3}cosθ）$，（θ∈（0，2π）），B₁P、B₂P的方程分别为：y=$\frac{\sqrt{3}cosθ+\sqrt{3}}{2sinθ}$x-$\sqrt{3}$，$y=\frac{\sqrt{3}cosθ-\sqrt{3}}{2sinθ}x+\sqrt{3}$．可得M，N．设经过M，N两点圆的圆心为Q（x₀，y₀），则x₀=$\frac{{x}_{M}+{x}_{N}}{2}$，半径r²=|QT|²=|QM|²，|OT|²=|OQ|²-|QT|²=${x}_{0}^{2}+{y}_{0}^{2}$-r²．

解答 解：（I）由题意可得：$\left\{\begin{array}{l}{\frac{c}{a}=\frac{1}{2}}\\{c=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$，解得c=1，a=2，b²=3．
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$；
（II）设P$（2sinθ，\sqrt{3}cosθ）$，（θ∈（0，2π）），
B₁P、B₂P的方程分别为：y=$\frac{\sqrt{3}cosθ+\sqrt{3}}{2sinθ}$x-$\sqrt{3}$，$y=\frac{\sqrt{3}cosθ-\sqrt{3}}{2sinθ}x+\sqrt{3}$．
可得M（$\frac{2sinθ}{cosθ+1}$，0），N$（\frac{2sinθ}{1-cosθ}，0）$．
设经过M，N两点圆的圆心为Q（x₀，y₀），则x₀=$\frac{{x}_{M}+{x}_{N}}{2}$=$\frac{2}{sinθ}$，
半径r²=|QT|²=|QM|²=$（\frac{2}{sinθ}-\frac{2sinθ}{1+cosθ}）^{2}$+${y}_{0}^{2}$，
|OT|²=|OQ|²-|QT|²=${x}_{0}^{2}+{y}_{0}^{2}$-r²=$（\frac{2}{sinθ}）^{2}-$$（\frac{2}{sinθ}-\frac{2sinθ}{1+cosθ}）^{2}$=$\frac{8}{1+cosθ}$-$（\frac{2sinθ}{1+cosθ}）^{2}$=$\frac{8（1+cosθ）-4si{n}^{2}θ}{（1+cosθ）^{2}}$=$\frac{4+4cosθ}{1+cosθ}$=4．

点评 本题考查了椭圆的标准方程及其性质、椭圆的参数方程应用、圆的性质、勾股定理，考查了推理能力与计算能力，属于难题．