题目内容
(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
已知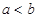 ,且
,且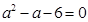 ,
,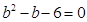 ,数列
,数列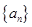 、
、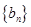 满足
满足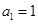 ,
,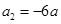 ,
,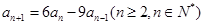 ,
,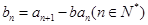 .
.
(1) 求证数列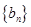 是等比数列;
是等比数列;
(2) (理科)求数列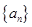 的通项公式
的通项公式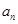 ;
;
(3) (理科)若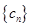 满足
满足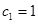 ,
,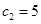 ,
,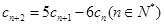 ,试用数学归纳法证明:
,试用数学归纳法证明:
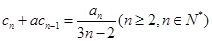 .
.
已知
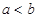 ,且
,且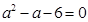 ,
,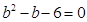 ,数列
,数列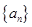 、
、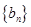 满足
满足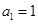 ,
,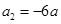 ,
,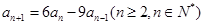 ,
,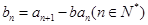 .
.(1) 求证数列
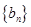 是等比数列;
是等比数列;(2) (理科)求数列
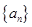 的通项公式
的通项公式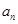 ;
;(3) (理科)若
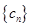 满足
满足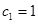 ,
,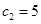 ,
,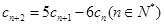 ,试用数学归纳法证明:
,试用数学归纳法证明: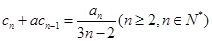 .
.证明(1)∵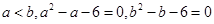 ,
,
∴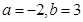 ,
,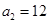 .
.
∵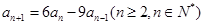 ,
,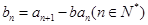 ,
,
∴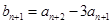
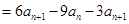
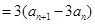
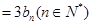 .
.
又 ,
,
∴数列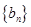 是公比为3,首项为
是公比为3,首项为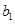 的等比数列.
的等比数列.
解(2)(理科)依据(1 )可以,得
)可以,得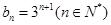 .
.
于是,有 ,即
,即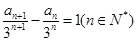 .
.
因此,数列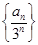 是首项为
是首项为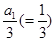 ,公差为1的等差数列.
,公差为1的等差数列.
故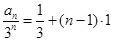 .
.
所以数列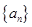 的通项公式是
的通项公式是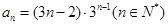 .
.
(3)(理科)用数学归纳法证明: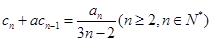
(i)当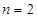 时,左边
时,左边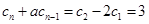 ,右边
,右边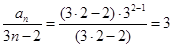 ,
,
即左边=右边,所以当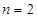 时结论成立.
时结论成立.
(ii)假设当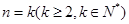 时,结论成立,即
时,结论成立,即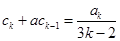 .
.
当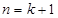 时,左边
时,左边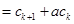
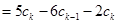
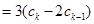
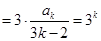 ,
,
右边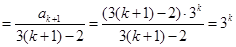 .
.
即左边=右边,因此,当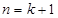 时,结论也成立.
时,结论也成立.
根据(i)、(ii)可以断定,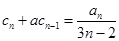 对
对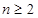 的正整数都成立.
的正整数都成立.
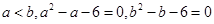 ,
,∴
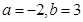 ,
,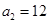 .
. ∵
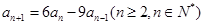 ,
,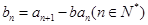 ,
,∴
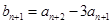
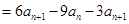
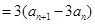
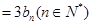 .
. 又
 ,
,∴数列
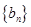 是公比为3,首项为
是公比为3,首项为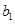 的等比数列.
的等比数列. 解(2)(理科)依据(1
 )可以,得
)可以,得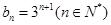 .
.于是,有
 ,即
,即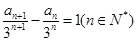 .
. 因此,数列
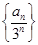 是首项为
是首项为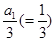 ,公差为1的等差数列.
,公差为1的等差数列.故
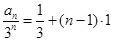 .
.所以数列
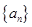 的通项公式是
的通项公式是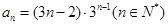 .
. (3)(理科)用数学归纳法证明:
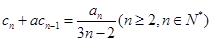
(i)当
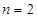 时,左边
时,左边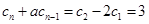 ,右边
,右边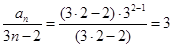 ,
,即左边=右边,所以当
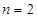 时结论成立.
时结论成立. (ii)假设当
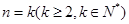 时,结论成立,即
时,结论成立,即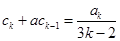 .
. 当
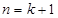 时,左边
时,左边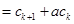
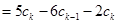
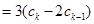
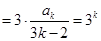 ,
,右边
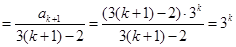 .
.即左边=右边,因此,当
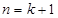 时,结论也成立.
时,结论也成立. 根据(i)、(ii)可以断定,
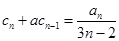 对
对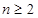 的正整数都成立.
的正整数都成立.略

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
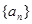 ,
,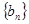 满足:
满足: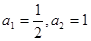 ,
,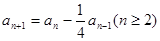 ;
;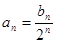 (
(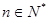 )
)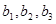 ,并求数列
,并求数列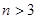 ,都有
,都有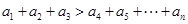 .
.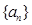 中,首项
中,首项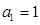 ,数列
,数列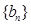 满足
满足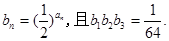
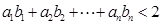 .
.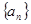 满足:
满足: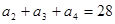 ,且
,且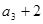 是
是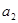 和
和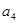 的等差中项.
的等差中项. ;
;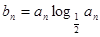 ,
,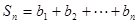 ,求使
,求使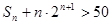 成立的小的正整数
成立的小的正整数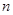 .
.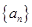 是等差数列,
是等差数列,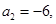
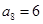 ,Sn是数列
,Sn是数列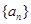 的前
的前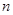 项和为
项和为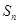 ,且
,且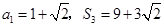 .
.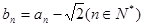 ,
,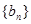 中的部分项
中的部分项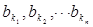 恰好组成等比数列,且
恰好组成等比数列,且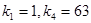 ,求该等比数列的公比与数列
,求该等比数列的公比与数列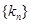 的通项公式。
的通项公式。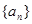 的前13项之和为
的前13项之和为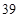 ,则
,则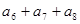 等于( )
等于( )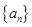 中,
中,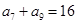 ,
,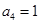 ,则
,则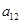 的值是( )
的值是( )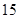
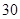
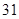
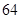
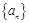 的前
的前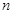 项和为
项和为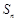 ,
,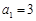 ,且当
,且当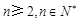 时
时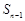 是
是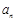 与
与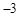 的等差中项,则数列
的等差中项,则数列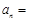 .
.