题目内容

精英家教网设函数f(x)=
-x2-2x+15
，集合A={x|y=f（x）}，B={y|y=f（x）}，则右图中阴影部分表示的集合为（　　）
A、[0，3]
B、（0，3）
C、（-5，0]∪[3，4）
D、[-5，0）∪（3，4]
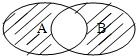
分析：本题考查的知识点是Venn图表达集合的关系及运算及函数定义域和值域的求法，由集合A={x|y=f（x）}，B={y|y=f（x）}，集合A，B分别表示函数f(x)=
-x2-2x+15
的定义域和值域，求出集合A与B后，分析韦恩图表示的含义，即可得到结果．
解答：解：由-x2-2x+15≥0
即x2+2x-15≤0，
得-5≤x≤3，
故A=[-5，3]．
由f(x)=
-x2-2x+15
=
-(x+1)2+16
∈[0，4]，
得B=[0，4]．
从而A∪B=[-5，4]，
A∩B=[0，3]．
阴影部分表示由在A∪B内且不在A∩B内的元素构成的集合，
故答案选D．
点评：本小题考查集合的概念、函数的定义域和值域等知识，并通过韦恩图“隐性”考查集合的交、并、补等基本运算，题目设置巧妙，令人耳目一新．审题时，要注意集合A和B是不同的，分别表示函数f（x）的定义域和值域．
练习册系列答案
相关题目
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
设函数f（x）=p（x-
1
x
）-2lnx，g（x）=
2e
x
（p是实数，e为自然对数的底数）
（1）若f（x）在其定义域内为单调函数，求p的取值范围；
（2）若直线l与函数f（x），g（x）的图象都相切，且与函数f（x）的图象相切于点（1，0），求p的值；
（3）若在[1，e]上至少存在一点x0，使得f（x0）＞g（x0）成立，求p的取值范围．
设函数f（x）的定义域为D，若存在非零实数l使得对于任意x∈M（M⊆D），有x+l∈D，且f（x+1）≥f（x），则称f（x）为M上的高调函数．现给出下列三个命题：
①函数f(x)=(
12
)x为R上的l高调函数；
②函数f（x）=sin2x为R上的π高调函数；
③如果定义域是[-1，+∞）的函数f（x）=x2为[-1，+∞）上的m高调函数，那么实数m的取值范围[2，+∞）；
其中正确的命题是
②③
②③
（填序号）
设函数f（x）是定义在R上的偶函数，且f（x+2）=f（x）恒成立；当x∈[0，1]时，f（x）=x3-4x+3．有下列命题：
①f(-
3
4
) ＜f(
15
2
)；
②当x∈[-1，0]时f（x）=x3+4x+3；
③f（x）（x≥0）的图象与x轴的交点的横坐标由小到大构成一个无穷等差数列；
④关于x的方程f（x）=|x|在x∈[-3，4]上有7个不同的根．
其中真命题的个数为（　　）
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网