题目内容
已知点B(5,0)和点C(-5,0),过点B的直线l与过点C的直线m相交于点A,设直线l的斜率为k1,直线m的斜率为k2:
(Ⅰ)如果k1•k2=
,求点A的轨迹方程;
(Ⅱ)如果k1•k2=a,其中a≠0,求点A的轨迹方程,并根据a的取值讨论此轨迹是何种曲线.
(Ⅰ)如果k1•k2=
| 16 |
| 25 |
(Ⅱ)如果k1•k2=a,其中a≠0,求点A的轨迹方程,并根据a的取值讨论此轨迹是何种曲线.
(Ⅰ)设点A(x,y),则 k1=
,k2=
,由 k1•k2=
,得
•
=
,
即
-
=1(y≠0).
(Ⅱ)由(Ⅰ)知 k1=
,k2=
,代入 k1•k2=a可得;
•
=a,即
-
=1(y≠0).
①当a>0,表示双曲线,去掉(5,0),(-5,0)两点.
②当-1<a<0,表示焦点在x轴上的椭圆.
③当 a=-1,表示圆.
④当a<-1,表示焦点在y轴的椭圆.
| y-0 |
| x-5 |
| y-0 |
| x+5 |
| 16 |
| 25 |
| y |
| x-5 |
| y |
| x+5 |
| 16 |
| 25 |
即
| x2 |
| 25 |
| y2 |
| 16 |
(Ⅱ)由(Ⅰ)知 k1=
| y-0 |
| x-5 |
| y-0 |
| x+5 |
| y |
| x-5 |
| y |
| x+5 |
| x2 |
| 25 |
| y2 |
| 25a |
①当a>0,表示双曲线,去掉(5,0),(-5,0)两点.
②当-1<a<0,表示焦点在x轴上的椭圆.
③当 a=-1,表示圆.
④当a<-1,表示焦点在y轴的椭圆.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
 ,求点A的轨迹方程;
,求点A的轨迹方程;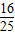 ,求点A的轨迹方程;
,求点A的轨迹方程;