题目内容
已知点B(5,0)和点C(-5,0),过点B的直线l与过点C的直线m相交于点A,设直线l的斜率为k1,直线m的斜率为k2:(Ⅰ)如果k1•k2=
| 16 | 25 |
(Ⅱ)如果k1•k2=a,其中a≠0,求点A的轨迹方程,并根据a的取值讨论此轨迹是何种曲线.
分析:(Ⅰ)设点A(x,y),用x,y表示 k1和k2 ,利用 k1•k2=
,建立关于x,y的方程.
(Ⅱ) 用x,y表示 k1和k2 ,k1•k2=a,建立关于x,y的方程并进行化简,讨论a的取值范围,确定轨迹所代表的曲线.
| 16 |
| 25 |
(Ⅱ) 用x,y表示 k1和k2 ,k1•k2=a,建立关于x,y的方程并进行化简,讨论a的取值范围,确定轨迹所代表的曲线.
解答:解:(Ⅰ)设点A(x,y),则 k1=
,k2=
,由 k1•k2=
,得
•
=
,
即
-
=1(y≠0).
(Ⅱ)由(Ⅰ)知 k1=
,k2=
,代入 k1•k2=a可得;
•
=a,即
-
=1(y≠0).
①当a>0,表示双曲线,去掉(5,0),(-5,0)两点.
②当-1<a<0,表示焦点在x轴上的椭圆.
③当 a=-1,表示圆.
④当a<-1,表示焦点在y轴的椭圆.
| y-0 |
| x-5 |
| y-0 |
| x+5 |
| 16 |
| 25 |
| y |
| x-5 |
| y |
| x+5 |
| 16 |
| 25 |
即
| x2 |
| 25 |
| y2 |
| 16 |
(Ⅱ)由(Ⅰ)知 k1=
| y-0 |
| x-5 |
| y-0 |
| x+5 |
| y |
| x-5 |
| y |
| x+5 |
| x2 |
| 25 |
| y2 |
| 25a |
①当a>0,表示双曲线,去掉(5,0),(-5,0)两点.
②当-1<a<0,表示焦点在x轴上的椭圆.
③当 a=-1,表示圆.
④当a<-1,表示焦点在y轴的椭圆.
点评:本题考查求点的轨迹方程的方法,以及由轨迹方程判断轨迹所代表的曲线,体现了分类讨论的数学思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,求点A的轨迹方程;
,求点A的轨迹方程;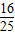 ,求点A的轨迹方程;
,求点A的轨迹方程;