题目内容
观察等式sin215°+sin275°+sin245°=| 3 |
| 2 |
| 3 |
| 2 |
分析:分析已知条件中:sin215°+sin275°+sin245°=
,sin210°+sin270°+sin250°=
,我们可以发现等式左边参加累加的三个均为正弦的平方,且三个角组成一个以60°为公差的等差数列,右边是常数,由此不难得到结论.
| 3 |
| 2 |
| 3 |
| 2 |
解答:解:一般化的正确等式为sin2x°+sin2(60°+x°)+sin2(60°-x°)=
.(5分)
证明:sin2x°+sin2(60°+x°)+sin2(60°-x°)
=
+
+
(8分)
=
+
+
(12分)
=
=
.(14分)
| 3 |
| 2 |
证明:sin2x°+sin2(60°+x°)+sin2(60°-x°)
=
| 1-cos(2x)° |
| 2 |
| 1-cos(120°+(2x)°) |
| 2 |
| 1-cos(120°-(2x)°) |
| 2 |
=
| 1-cos(2x)° |
| 2 |
| 1-cos120°cos(2x)°+sin120°sin(2x)° |
| 2 |
| 1-cos120°cos(2x)°-sin120°sin(2x)° |
| 2 |
=
1-cos2x°+1+
| ||||
| 2 |
| 3 |
| 2 |
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想),(3)论证.

练习册系列答案
相关题目



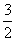 ,sin210°+sin270°+sin250°=
,sin210°+sin270°+sin250°=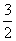 ,请写出与以上等式规律相同的一个一般化的正确等式,并给予证明。
,请写出与以上等式规律相同的一个一般化的正确等式,并给予证明。