题目内容
已知首项为x1的数列{xn}满足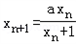
（a为常数）．
（1）若对于任意的x1≠﹣1，有xn+2=xn对于任意的n∈N*都成立，求a的值；
（2）当a=1时，若x1＞1，数列{xn}是递增数列还是递减数列？请说明理由；
（3）当a确定后，数列{xn}由其首项x1确定，当a=2时，通过对数列{xn}的探究，写出“{xn}是有穷数列”的一个真命题（不必证明）．
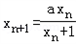（a为常数）．（1）若对于任意的x1≠﹣1，有xn+2=xn对于任意的n∈N*都成立，求a的值；
（2）当a=1时，若x1＞1，数列{xn}是递增数列还是递减数列？请说明理由；
（3）当a确定后，数列{xn}由其首项x1确定，当a=2时，通过对数列{xn}的探究，写出“{xn}是有穷数列”的一个真命题（不必证明）．
解：（1）∵xn+2=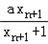
=
=
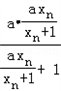=xn
∴a2xn=（a+1）xn2+xn，
当n=1时，由x1的任意性得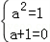
，
∴a=﹣1．
（2）数列{xn}是递减数列．
∵x1＞0.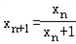
∴xn＞0，n∈N*
又xn+1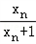﹣xn=
﹣xn=﹣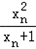
＜0，n∈N*，
故数列{xn}是递减数列．
（3）满足条件的真命题为：数列{xn}满足xn+1=
，若x1=﹣
，则{xn}是有穷数列．
===xn∴a2xn=（a+1）xn2+xn，
当n=1时，由x1的任意性得
，∴a=﹣1．
（2）数列{xn}是递减数列．
∵x1＞0.
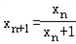
∴xn＞0，n∈N*
又xn+1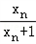﹣xn=
﹣xn=﹣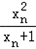＜0，n∈N*，故数列{xn}是递减数列．
（3）满足条件的真命题为：数列{xn}满足xn+1=
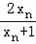，若x1=﹣，则{xn}是有穷数列．
练习册系列答案
相关题目
（a为常数）．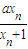
（a为常数）．
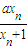（a为常数）．