题目内容
15.已知点(-$\frac{π}{8}$,0)为函数f(x)=3sin(2x+φ)的一个对称中心,且-$\frac{π}{2}$<φ<$\frac{π}{2}$.(Ⅰ)求φ的值及函数f(x)的单调减区间;
(Ⅱ)求f(x)在区间[0,$\frac{π}{2}$]上的最大值及f(x)取最大值时x的值.
分析 (1)首先,根据对称中心,代入即可得到相应的φ=$\frac{π}{4}$,然后,根据正弦函数的单调性确定其单调减区间;
(2)直接根据(1)的结果,利用正弦函数的图象确定其最大值即可.
解答 解:(1)∵点(-$\frac{π}{8}$,0)为函数f(x)=3sin(2x+φ)的一个对称中心,
∴将点(-$\frac{π}{8}$,0)代入f(x)=3sin(2x+φ)得,
3sin(-$\frac{π}{4}$+φ)=0,
∵-$\frac{π}{2}$<φ<$\frac{π}{2}$.
∴φ=$\frac{π}{4}$,
∴f(x)=3sin(2x+$\frac{π}{4}$),
令$\frac{π}{2}$+2kπ≤2x+$\frac{π}{4}$≤$\frac{3π}{2}$+2kπ,k∈Z,
∴$\frac{π}{4}$+2kπ≤2x≤$\frac{5π}{4}$+2kπ,
∴$\frac{π}{8}$+kπ≤x≤$\frac{5π}{8}$+kπ,
∴函数f(x)的单调减区间[$\frac{π}{8}$+kπ,$\frac{5π}{8}$+kπ],
(2)∵0≤x≤$\frac{π}{2}$,
∴0≤2x≤π,
∴$\frac{π}{4}$≤2x+$\frac{π}{4}$≤$\frac{5π}{4}$,
∴当2x+$\frac{π}{4}$=$\frac{π}{2}$,即x=$\frac{π}{8}$时,该函数取得最大值为:3.
点评 本题重点考查了三角函数的图象与性质、三角函数单调性与最值问题的处理思路和方法,属于中档题.

练习册系列答案
相关题目
20.已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.若B⊆A,则实数m的取值范围为( )
| A. | m≤3 | B. | 2≤m≤3 | C. | m≥2 | D. | m≥3 |
7.已知函数f(x)=(m2-m-1)x-5m-1是幂函数且是(0,+∞)上的增函数,则m的值为( )
| A. | 2 | B. | -1 | C. | -1或2 | D. | 0 |
5.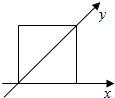 对某平面图形使用斜二测画法后得到的直观图是边长为1的正方形(如图),则原图形的面积是( )
对某平面图形使用斜二测画法后得到的直观图是边长为1的正方形(如图),则原图形的面积是( )
 对某平面图形使用斜二测画法后得到的直观图是边长为1的正方形(如图),则原图形的面积是( )
对某平面图形使用斜二测画法后得到的直观图是边长为1的正方形(如图),则原图形的面积是( )| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |