题目内容

（2012•潍坊二模）为了普及环保知识，增强环保意识，某大学从理工类专业的A班和文史类专业的B班各抽取20名同学参加环保知识测试．统计得到成绩与专业的列联表：
优秀 非优秀 总计
A班 14 6 20
B班 7 13 20
C班 21 19 40
附：参考公式及数据：
（1）卡方统计量x2=
n(n11n22-n12n21)2
(n11+n12)(n21+n22)(n11+n21)(n12+n22)
（其中n=n11+n12+n21+n22）；
（2）独立性检验的临界值表：
P（x2≥k0） 0.050 0.010
K0 3.841 6.635
则下列说法正确的是（　　）
分析：由列联表中数据，代入公式，求出X2的值，进而与3.841进行比较，即可得出能否有95%的把握认为环保知识测试成绩与专业有关．
解答：解：由两个班同学的统计得到成绩与专业的列联表：

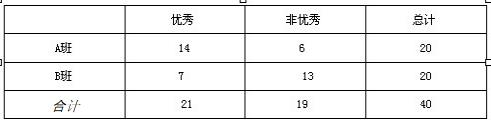
根据列联表中的数据可得
X2=40（14×13-6×7）2÷（21×19×20×20）≈4.912＞3.841
∴有95%的把握认为环保知识测试成绩与专业有关．
故选C．
点评：本题考查独立性检验的应用，考查数据处理能力、运算求解能力和应用意识，本题解题的关键是正确运算出观测值，理解临界值对应的概率的意义，要想知道两个变量之间的有关或无关的精确的可信程度，只有利用独立性检验的有关计算，才能做出判断，本题是一个基础题．
练习册系列答案
相关题目
（2012•潍坊二模）①函数y=sin(x-
π
2
)在[0，π]上是减函数；
②点A（1，1）、B（2，7）在直线3x-y=0两侧；
③数列{an}为递减的等差数列，a1+a5=0，设数列{an}的前n项和为Sn，则当n=4时，Sn取得最大值；
④定义运算
.
a1
b1
a2
b2
.
=a1b2-a2b1则函数f(x)=
.
x2+3x
x
1
1
3
x
.
的图象在点(1，
1
3
)处的切线方程是6x-3y-5=0．
其中正确命题的序号是
②④
②④
（把所有正确命题的序号都写上）．
（2012•潍坊二模）已知两条直线a，b与两个平面α、β，b⊥α，则下列命题中正确的是（　　）
①若a∥α，则a⊥b；
②若a⊥b，则a∥α； 
③若b⊥β，则α∥β；
④若α⊥β，则b∥β．
（2012•潍坊二模）已知向量
a
=（x，-2），
b
=（y，1），其中x，y都是正实数，若
a
⊥
b
，则t=x+2y的最小值是
4
4
．
（2012•潍坊二模）已知函数f（x）的图象向左平移1个单位后关于y轴对称，当x2＞x1＞1时，[f（x2）-f（x1）]（x2-x1）＜0恒成立，设a=f（-
1
2
），b=f（2），c=f（3），则a、b、c的大小关系为（　　）
（2012•潍坊二模）已知双曲线C：
x2
4
-
y2
5
=1的左、右焦点分别为F1、F2，P为C的右支上一点，且|PF2|=|F1F2|，则
PF1
•
PF2
等于（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网