Question

已知函数的两条切线PM、PN，切点分别为M、N.

   （I）当时，求函数的单调递增区间；

   （II）设|MN|=，试求函数的表达式；

   （III）在（II）的条件下，若对任意的正整数，在区间内，总存在m＋1个数使得不等式成立，求m的最大值.

Answer 1

（Ⅰ）（Ⅱ）

（Ⅲ）m的最大值为6

解析:

（I）当  …………………1分

       .则函数有单调递增区间为………2分

   （II）设M、N两点的横坐标分别为、，

…………………4分

      

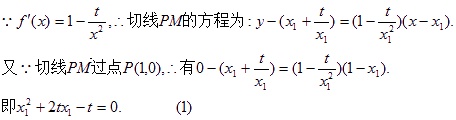
       同理，由切线PN也过点（1，0），得 （2）

       由（1）、（2），可得的两根，

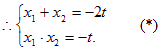       …………………………………………………………6分

      

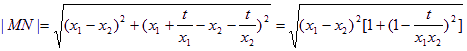
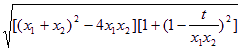
       把（*）式代入，得

       因此，函数…………………8分

   （III）易知上为增函数，

      

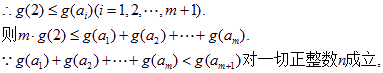
       ……………10分

      

      

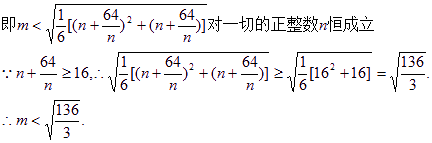
       由于m为正整数，.……………………………………………………13分

       又当

       因此，m的最大值为6.