题目内容
(本题满分12分)设函数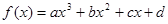 (a、b、c、d∈R)满足:
(a、b、c、d∈R)满足:
对任意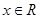 都有
都有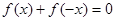 ,
,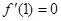 ,
,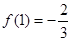
(1)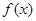 的解析式;
的解析式;
(2)当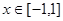 时,证明:函数图象上任意两点处的切线不可能互相垂直;
时,证明:函数图象上任意两点处的切线不可能互相垂直;
(3)设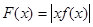 ,证明:
,证明: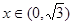 时,
时,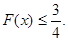
【答案】
解:(I)因为,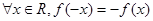 成立,所以:
成立,所以: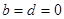 ,
,
由: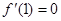 ,得
,得 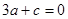 ,
,
由: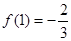 ,得
,得 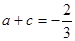
解之得: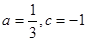 从而,函数解析式为:
从而,函数解析式为: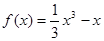 …………4分
…………4分
(2)由于,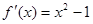 ,设:任意两数
,设:任意两数 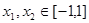 是函数
是函数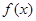 图像上两点的横坐
图像上两点的横坐
标,则这两点的切线的斜率分别是: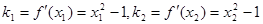
又因为: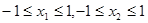 ,所以,
,所以,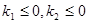 ,得:
,得: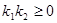 知:
知:
故,当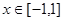 是函数
是函数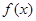 图像上任意两点的切线不可能垂直…………9分
图像上任意两点的切线不可能垂直…………9分
(3)当: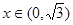 时,
时,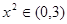 且
且 此时
此时
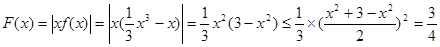
当且仅当: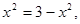 即
即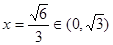 ,取等号,故:
,取等号,故: …………12分
…………12分
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数 .
. 为真,求实数
为真,求实数 .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集;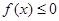 的解集为
的解集为 ,求a的值。
,求a的值。
 与
与 垂直,求
垂直,求 的值
的值  的最大值;
的最大值;  ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 与
与 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列, 满足
满足 ,求
,求