题目内容
2.已知函数y=f(x)=Asin(wx+φ)(A>0,w>0,|φ|<π),满足以下条件:①对任意x∈R,恒有f(x)≤f($\frac{5π}{6}$)=2;
②若f(α)=0,|α-$\frac{5π}{6}$|的最小值为$\frac{π}{4}$.
(1)求函数f(x)的解析式;
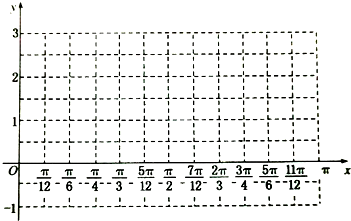
(2)画出函数y=f(x)在区间[0,π]内的图象.
分析 (1)根据函数的性质求出A,ω和φ的值,即可求函数f(x)的解析式;
(2)利用五点法即可画出函数y=f(x)在区间[0,π]内的图象
解答 解:(1)∵①对任意x∈R,恒有f(x)≤f($\frac{5π}{6}$)=2;
∴A=2,x=$\frac{5π}{6}$是函数的对称轴,
∵②若f(α)=0,|α-$\frac{5π}{6}$|的最小值为$\frac{π}{4}$.
∴$\frac{T}{4}$=$\frac{π}{4}$,
即函数的周期T=π=$\frac{2π}{ω}$,
即ω=2,则f(x)=2sin(2x+φ),
∵f($\frac{5π}{6}$)=2;
∴2sin(2×$\frac{5π}{6}$+φ)=2;
即sin($\frac{5π}{3}$+φ)=1;
则$\frac{5π}{3}$+φ=$\frac{π}{2}$+2kπ,k∈Z,
即φ=2kπ-$\frac{7π}{6}$,
∵|φ|<π,
∴当k=1时,φ=2π-$\frac{7π}{6}$=$\frac{5π}{6}$,
即函数f(x)的解析式f(x)=2sin(2x+$\frac{5π}{6}$);
(2)画出函数y=f(x)在区间[0,π]内的图象.
| x | 0 | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ | π |
| 2x+$\frac{5π}{6}$ | $\frac{5π}{6}$ | π | $\frac{3π}{2}$ | 2π | $\frac{5π}{2}$ | $\frac{17π}{6}$ |
| 2sin(2x+$\frac{5π}{6}$) | 1 | 0 | -2 | 0 | 2 | 1 |

点评 本题主要考查三角函数的图象,根据三角函数的性质求出函数的解析式以及利用五点法是解决本题的关键.

练习册系列答案
相关题目
11.不等式3x2-7x-6<0的解集是( )
| A. | $\left\{{x|x<-\frac{2}{3}或x>3}\right\}$ | B. | $\left\{{x|x<-3或x>\frac{2}{3}}\right\}$ | C. | $\left\{{x|-3<x<\frac{2}{3}}\right\}$ | D. | $\left\{{x|-\frac{2}{3}<x<3}\right\}$ |
12.在△ABC中,$\overrightarrow{AB}$=($\sqrt{3}$,-1),$\overrightarrow{BC}$=(1,-$\sqrt{3}$),则cosB=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | 0 |