题目内容
【题目】已知全集U=R,集合A={x|2x+a>0},B={x|x2﹣2x﹣3>0}. (Ⅰ)当a=2时,求集合A∩B;
(Ⅱ)若A∩(UB)=,求实数a的取值范围.
【答案】解:由2x+a>0得 ![]() ,即
,即 ![]() . 由x2﹣2x﹣3>0得(x+1)(x﹣3)>0,解得x<﹣1或x>3,
. 由x2﹣2x﹣3>0得(x+1)(x﹣3)>0,解得x<﹣1或x>3,
即B={x|x<﹣1或x>3}.
(Ⅰ)当a=2时,A={x|x>﹣1}.
∴A∩B={x|x>3}.
(Ⅱ)∵B={x|x<﹣1或x>3},
∴UB={x|﹣1≤x≤3}.
又∵A∩(UB)=,
∴ ![]() ,
,
解得a≤﹣6.
∴实数a的取值范围是(﹣∞,﹣6]
【解析】(Ⅰ)当a=2时,求出集合A,利用集合的基本运算求A∩B.(Ⅱ)求出UB,然后根据集合关系A∩(UB)=,确定a的取值范围.

【题目】某畜牧站为了考查某种新型药物预防动物疾病的效果,利用小白鼠进行试验,得到如下丢失数据的![]() 列联表
列联表
患病 | 未患病 | 总计 | |
没服用药 | 20 | 30 | 50 |
服用药 |
|
| 50 |
总计 |
|
| 100 |
设从没服用药的小白鼠中任取两只,未患病的动物数为![]() ,从服用药物的小白鼠中任取两只,未患病的动物数为
,从服用药物的小白鼠中任取两只,未患病的动物数为![]() ,得到如下比例关系:
,得到如下比例关系:![]()
(1)求出![]() 列联表中数据
列联表中数据![]() ,
,![]() ,
,![]() ,
,![]() 的值
的值
(2)是否有![]() 的把握认为药物有效?并说明理由
的把握认为药物有效?并说明理由
(参考公式:![]() ,当
,当![]() 时,有
时,有![]() 的把握认为A与B有关;
的把握认为A与B有关;![]() 时,有
时,有![]() 的把握认为A与B有关.
的把握认为A与B有关.
【题目】为了调查“五一”小长假出游选择“有水的地方”是否与性别有关,现从该市“五一”出游旅客中随机抽取500人进行调查,得到如下2×2列联表:(单位:人)
选择“有水的地方” | 不选择“有水的地方” | 合计 | |
男 | 90 | 110 | 200 |
女 | 210 | 90 | 300 |
合计 | 300 | 200 | 500 |
(Ⅰ)据此样本,有多大的把握认为选择“有水的地方”与性别有关;
(Ⅱ)若以样本中各事件的频率作为概率估计全市“五一”所有出游旅客情况,现从该市的全体出游旅客(人数众多)中随机抽取3人,设3人中选择“有水的地方”的人数为随机变量X,求随机变量X的数学期望和方差.
附临界值表及参考公式:
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
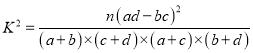 ,n=a+b+c+d.
,n=a+b+c+d.