题目内容
已知在三棱锥S-ABC中,底面是边长为4的正三角形,侧面SAC⊥底面ABC,M,N分别是AB,SB的中点,SA=SC=2
:
(1)求证AC⊥SB
(2)求二面角N-CM-B的大小
(3)求点B到面CMN的距离.
| 3 |
(1)求证AC⊥SB
(2)求二面角N-CM-B的大小
(3)求点B到面CMN的距离.
分析:(1)由题意取AC中点D,连接SD、DB.则可证AC⊥平面SDB,从而AC⊥SB;
(2)过N作NE⊥BD于E,NE⊥平面ABC,过E作EF⊥CM于F,连接NF,则NF⊥CM.从而∠NFE为二面角N-CM-B的平面角.在Rt△NEF中,利用正切函数,可求二面角N-CM-B的大小;
(3)设点B到平面CMN的距离为h,根据VB-CMN=VN-CMB,NE⊥平面CMB,可求点B到平面CMN的距离.
(2)过N作NE⊥BD于E,NE⊥平面ABC,过E作EF⊥CM于F,连接NF,则NF⊥CM.从而∠NFE为二面角N-CM-B的平面角.在Rt△NEF中,利用正切函数,可求二面角N-CM-B的大小;
(3)设点B到平面CMN的距离为h,根据VB-CMN=VN-CMB,NE⊥平面CMB,可求点B到平面CMN的距离.
解答: 解:(1)取AC中点D,连接SD、DB.
解:(1)取AC中点D,连接SD、DB.
∵SA=SC,AB=BC,
∴AC⊥SD且AC⊥BD,
∵SD∩BD=D
∴AC⊥平面SDB,
又SB?平面SDB,
∴AC⊥SB.
(2)∵AC⊥平面SDB,AC?平面ABC,
∴平面SDB⊥平面ABC.
过N作NE⊥BD于E,NE⊥平面ABC,
过E作EF⊥CM于F,连接NF,
则NF⊥CM.
∴∠NFE为二面角N-CM-B的平面角.
∵平面SAC⊥平面ABC,SD⊥AC,∴SD⊥平面ABC.
又∵NE⊥平面ABC,∴NE∥SD.
∵SN=NB,∴NE=
SD=
=
=
,且ED=EB.
在正△ABC中,由平几知识可求得EF=
MB=
,
在Rt△NEF中,tan∠NFE=
=2
,
∴二面角N-CM-B的大小是arctan2
.
(3)在Rt△NEF中,NF=
=
,
∴S△CMN=
CM•NF=
,S△CMB=
BM•CM=2
.
设点B到平面CMN的距离为h,
∵VB-CMN=VN-CMB,NE⊥平面CMB,
∴
S△CMN•h=
S△CMB•NE,
∴h=
=
.即点B到平面CMN的距离为
.
 解:(1)取AC中点D,连接SD、DB.
解:(1)取AC中点D,连接SD、DB.∵SA=SC,AB=BC,
∴AC⊥SD且AC⊥BD,
∵SD∩BD=D
∴AC⊥平面SDB,
又SB?平面SDB,
∴AC⊥SB.
(2)∵AC⊥平面SDB,AC?平面ABC,
∴平面SDB⊥平面ABC.
过N作NE⊥BD于E,NE⊥平面ABC,
过E作EF⊥CM于F,连接NF,
则NF⊥CM.
∴∠NFE为二面角N-CM-B的平面角.
∵平面SAC⊥平面ABC,SD⊥AC,∴SD⊥平面ABC.
又∵NE⊥平面ABC,∴NE∥SD.
∵SN=NB,∴NE=
| 1 |
| 2 |
| 1 |
| 2 |
| SA2-AD2 |
| 1 |
| 2 |
| 12-4 |
| 2 |
在正△ABC中,由平几知识可求得EF=
| 1 |
| 4 |
| 1 |
| 2 |
在Rt△NEF中,tan∠NFE=
| EN |
| EF |
| 2 |
∴二面角N-CM-B的大小是arctan2
| 2 |
(3)在Rt△NEF中,NF=
| EF2+EN2 |
| 3 |
| 2 |
∴S△CMN=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
设点B到平面CMN的距离为h,
∵VB-CMN=VN-CMB,NE⊥平面CMB,
∴
| 1 |
| 3 |
| 1 |
| 3 |
∴h=
| S△CMB•NE |
| S△CMN |
| 4 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2 |
点评:本题以三棱锥为载体,考查线面垂直,线线垂直,考查面面角,考查点面距离,同时考查等体积转化思想.解题的关键是正确运用线面垂直的判定,正确作出面面角,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 :
: :
: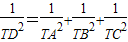 ;
; (注:S△ABC表示△ABC的面积)
(注:S△ABC表示△ABC的面积)