题目内容
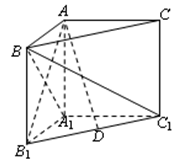
如图,在直三棱柱 (侧棱和底面垂直的棱柱)中,平面
(侧棱和底面垂直的棱柱)中,平面 侧面
侧面 ,
,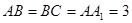 ,
, ,且满足
,且满足 .
.
(1)求证: ;
;
(2)求点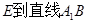 的距离;
的距离;
(3)求二面角 的平面角的余弦值.
的平面角的余弦值.
(1)详见解析;(2)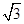 ;(3)
;(3) .
.
解析试题分析:(1)过点A在平面A1ABB1内作AD⊥A1B于D,然后根据条件平面 侧面
侧面 得到AD⊥平面A1BC,从而得到AD⊥BC.再结合直三棱柱的定义得到AA1⊥BC.所以BC⊥侧面A1ABB1,最后由线面垂直的定义得到结论;(2)BC、BA、BB1所在的直线两两相互垂直,所以可建立空间直角坐标系,根据条件分别得到
得到AD⊥平面A1BC,从而得到AD⊥BC.再结合直三棱柱的定义得到AA1⊥BC.所以BC⊥侧面A1ABB1,最后由线面垂直的定义得到结论;(2)BC、BA、BB1所在的直线两两相互垂直,所以可建立空间直角坐标系,根据条件分别得到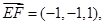
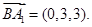 所以
所以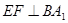 ,即点
,即点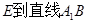 的距离
的距离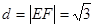 ;(3)分别计算平面
;(3)分别计算平面 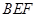 的法向量为
的法向量为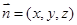 及平面
及平面 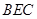 的法向量.其中平面
的法向量.其中平面 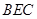 的法向量易知可以为
的法向量易知可以为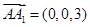 .然后再计算这两个法向量的夹角,则所求的二面角为该夹角或其补角.由图可知二面角
.然后再计算这两个法向量的夹角,则所求的二面角为该夹角或其补角.由图可知二面角 的平面角为钝角,故应为此夹角的补角,所以算得其余弦值为
的平面角为钝角,故应为此夹角的补角,所以算得其余弦值为 .
.
试题解析:(1)证明:如右图,过点A在平面A1ABB1内作
AD⊥A1B于D,则由平面A1BC⊥侧面A1ABB1,且平面A1BC 侧面A1ABB1=A1B,得
侧面A1ABB1=A1B,得
AD⊥平面A1BC,又BC 平面A1BC,所以AD⊥BC.
平面A1BC,所以AD⊥BC.
因为三棱柱ABC—A1B1C1是直三棱柱,则AA1⊥底面ABC,所以AA1⊥BC.
又AA1 AD=A,从而BC⊥侧面A1ABB1,
AD=A,从而BC⊥侧面A1ABB1,
又AB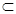 侧面A1ABB1,故AB⊥BC. 4分
侧面A1ABB1,故AB⊥BC. 4分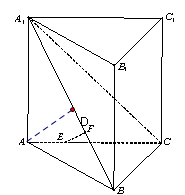
(2)由(1)知,以点B为坐标原点,以BC、BA、BB1所在的直线分
别为x轴、y轴、z轴,可建立如图所示的空间直角坐标系,
B(0,0,0), A(0,3,0), C(3,0,0) , 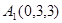
有由 ,满足
,满足 ,
,
所以E(1,2,0), F(0,1,1)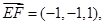
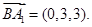 所以
所以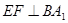 ,
,
所以点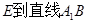 的距离
的距离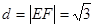 . 8分
. 8分
(3)设平面 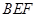 的法向量为
的法向量为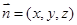 ,易知平面
,易知平面 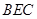 的法向量可以为
的法向量可以为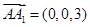 .
.
由 ,令
,令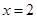 ,可得平面
,可得平面 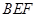 的一个法向量可为
的一个法向量可为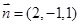 .设
.设 与
与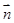 的夹角为
的夹角为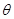 .则
.则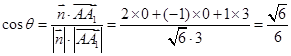 ,易知二面角
,易知二面角 的平面角为钝角,故应为角
的平面角为钝角,故应为角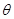 的补角,所以其余弦值为
的补角,所以其余弦值为 . 12分
. 12分
考点:1.直线与平面垂直的判定与性质;2.空间中点到直线的距离;3.二面角.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 垂直于底面ABCD,PA=AD=AB=2BC=2,M,N分别为PC,PB的中点.
垂直于底面ABCD,PA=AD=AB=2BC=2,M,N分别为PC,PB的中点.

 中,
中, 平面
平面 ,
, 是正三角形,
是正三角形, 与
与 的交点
的交点 恰好是
恰好是 ,
, ,点
,点 在线段
在线段 上,且
上,且 .
.
 ;
; 平面
平面 ;
; 的余弦值.
的余弦值. 面ABEF,且DA=1,AB//EF,
面ABEF,且DA=1,AB//EF,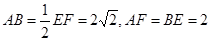 ,P、Q、M分别为AE、BD、EF的中点.
,P、Q、M分别为AE、BD、EF的中点.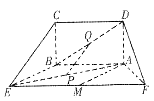
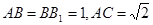 ,直线B1C与平面ABC成45°角。
,直线B1C与平面ABC成45°角。
 中,已知
中,已知 是棱
是棱 的中点.
的中点.
 平面
平面 ,
, ∥平面
∥平面 ;
;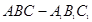 中,
中,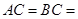
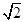 ,且
,且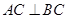 ,点
,点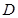 是
是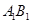 中点.
中点.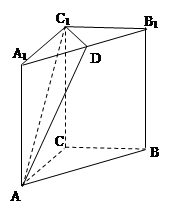
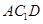 ⊥平面
⊥平面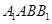 ;
;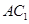 与平面
与平面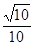 ,
,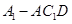 的体积.
的体积. 中,
中,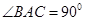 ,
,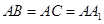 .
.
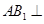 平面
平面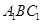 ;
; 为
为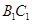 的中点,求
的中点,求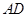 与平面
与平面