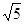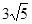题目内容
(本小题满分12分)在直角坐标系xOy中,曲线C1的点均在C2:(x-5)2+y2=9外,且对C1上任意一点M,M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值.
(1)求曲线C1的方程;
(2)设P(x0,y0)(y0≠±3)为圆C2外一点,过P作圆C2的两条切线,分别与曲线C1相交于
点A,B和C,D.证明:当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值.
(1)求曲线C1的方程;
(2)设P(x0,y0)(y0≠±3)为圆C2外一点,过P作圆C2的两条切线,分别与曲线C1相交于
点A,B和C,D.证明:当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值.
(1)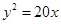 .
.
(2)当P在直线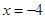 上运动时,四点A,B,C,D的纵坐标之积为定值6400.
上运动时,四点A,B,C,D的纵坐标之积为定值6400.
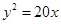 .
.(2)当P在直线
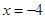 上运动时,四点A,B,C,D的纵坐标之积为定值6400.
上运动时,四点A,B,C,D的纵坐标之积为定值6400.(1) 曲线 上任意一点M到圆心
上任意一点M到圆心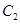
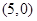 的距离等于它到直线
的距离等于它到直线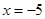 的距离,由抛物线的定义可知曲线C1为抛物线,此方程为
的距离,由抛物线的定义可知曲线C1为抛物线,此方程为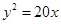 .
.
(2) 当点P在直线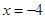 上运动时,设P的坐标为
上运动时,设P的坐标为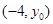 ,又
,又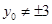 ,则过P且与圆
,则过P且与圆
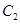 相切的切线方程为
相切的切线方程为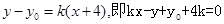 .则
.则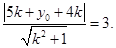
整理得
设过P所作的两条切线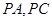 的斜率分别为
的斜率分别为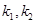 ,则
,则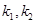 是方程①的两个实根,
是方程①的两个实根,
故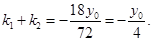
由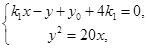 得
得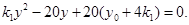
设四点A,B,C,D的纵坐标分别为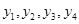 ,
,
则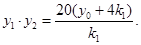 同理由
同理由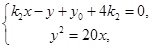 可得
可得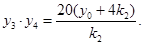
这样可得 ,然后展开将
,然后展开将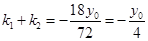 代入化简即可得到定值.
代入化简即可得到定值.
由题设知,曲线 上任意一点M到圆心
上任意一点M到圆心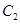
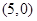 的距离等于它到直线
的距离等于它到直线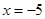 的距离,因此,曲线
的距离,因此,曲线 是以
是以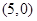 为焦点,直线
为焦点,直线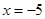 为准线的抛物线,故其方程为
为准线的抛物线,故其方程为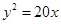 .
.
(2)当点P在直线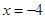 上运动时,P的坐标为
上运动时,P的坐标为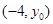 ,又
,又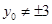 ,则过P且与圆
,则过P且与圆
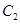 相切得直线的斜率
相切得直线的斜率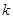 存在且不为0,每条切线都与抛物线有两个交点,切线方程为
存在且不为0,每条切线都与抛物线有两个交点,切线方程为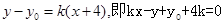 .
.
于是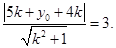
整理得 ①
①
设过P所作的两条切线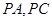 的斜率分别为
的斜率分别为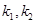 ,则
,则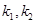 是方程①的两个实根,
是方程①的两个实根,
故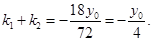 ②
②
由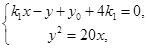 得
得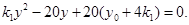 ③
③
设四点A,B,C,D的纵坐标分别为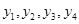 ,则是方程③的两个实根,
,则是方程③的两个实根,
所以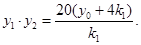 ④
④
同理可得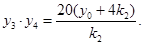 ⑤
⑤
于是由②,④,⑤三式得
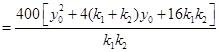
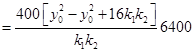 .
.
所以,当P在直线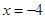 上运动时,四点A,B,C,D的纵坐标之积为定值6400.
上运动时,四点A,B,C,D的纵坐标之积为定值6400.
 上任意一点M到圆心
上任意一点M到圆心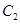
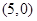 的距离等于它到直线
的距离等于它到直线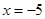 的距离,由抛物线的定义可知曲线C1为抛物线,此方程为
的距离,由抛物线的定义可知曲线C1为抛物线,此方程为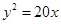 .
.(2) 当点P在直线
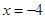 上运动时,设P的坐标为
上运动时,设P的坐标为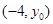 ,又
,又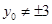 ,则过P且与圆
,则过P且与圆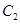 相切的切线方程为
相切的切线方程为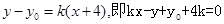 .则
.则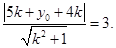
整理得

设过P所作的两条切线
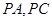 的斜率分别为
的斜率分别为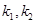 ,则
,则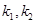 是方程①的两个实根,
是方程①的两个实根,故
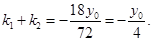
由
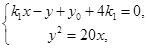 得
得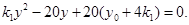
设四点A,B,C,D的纵坐标分别为
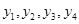 ,
,则
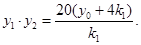 同理由
同理由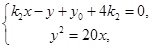 可得
可得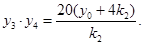
这样可得
 ,然后展开将
,然后展开将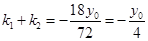 代入化简即可得到定值.
代入化简即可得到定值.由题设知,曲线
 上任意一点M到圆心
上任意一点M到圆心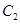
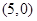 的距离等于它到直线
的距离等于它到直线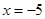 的距离,因此,曲线
的距离,因此,曲线 是以
是以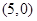 为焦点,直线
为焦点,直线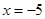 为准线的抛物线,故其方程为
为准线的抛物线,故其方程为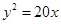 .
.(2)当点P在直线
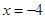 上运动时,P的坐标为
上运动时,P的坐标为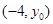 ,又
,又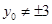 ,则过P且与圆
,则过P且与圆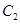 相切得直线的斜率
相切得直线的斜率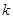 存在且不为0,每条切线都与抛物线有两个交点,切线方程为
存在且不为0,每条切线都与抛物线有两个交点,切线方程为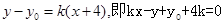 .
.于是
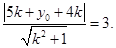
整理得
 ①
①设过P所作的两条切线
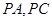 的斜率分别为
的斜率分别为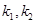 ,则
,则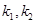 是方程①的两个实根,
是方程①的两个实根,故
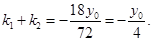 ②
②由
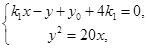 得
得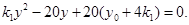 ③
③设四点A,B,C,D的纵坐标分别为
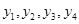 ,则是方程③的两个实根,
,则是方程③的两个实根,所以
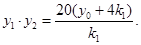 ④
④同理可得
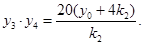 ⑤
⑤于是由②,④,⑤三式得

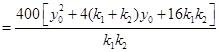
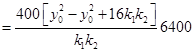 .
.所以,当P在直线
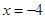 上运动时,四点A,B,C,D的纵坐标之积为定值6400.
上运动时,四点A,B,C,D的纵坐标之积为定值6400.
练习册系列答案
相关题目
 倍,求:(1)动点M的轨迹方程;(2)根据
倍,求:(1)动点M的轨迹方程;(2)根据 取值范围指出轨迹表示的图形.
取值范围指出轨迹表示的图形.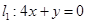 ,直线
,直线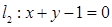 以及
以及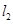 上一点
上一点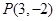 .
.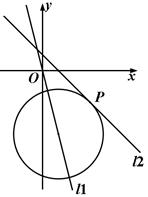
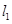 上且与直线
上且与直线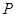 的圆⊙M的方程.
的圆⊙M的方程.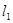 分别与直线
分别与直线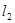 、圆⊙依次相交于A、B、C三点,
、圆⊙依次相交于A、B、C三点,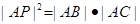 .
. 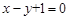 上,且经过圆
上,且经过圆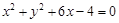 与圆
与圆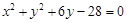 的交点的圆方程.
的交点的圆方程.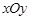 中,圆
中,圆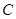 的方程为
的方程为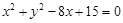 ,若直线
,若直线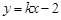 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆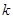 的最大值是 .
的最大值是 .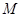 过两点
过两点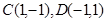 ,且圆心
,且圆心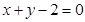 上.
上.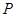 是直线
是直线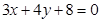 上的动点,
上的动点,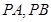 是圆
是圆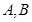 为切点,求四边形
为切点,求四边形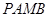 面积的最小值.
面积的最小值. 和圆
和圆 相交于点A、B,则AB的垂直平分线方程是
相交于点A、B,则AB的垂直平分线方程是 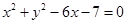 与抛物线
与抛物线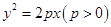 的准线相切,则
的准线相切,则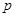 的值为()
的值为()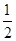
 上恰有两个点到直线
上恰有两个点到直线 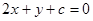 的距离等于1的
的距离等于1的 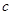 的一个可能值为( )
的一个可能值为( )