题目内容
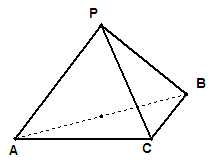
如图,在三棱锥 中,
中, 底面
底面 ,点
,点 ,
, 分别在棱
分别在棱 上,且
上,且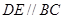

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)当 为
为 的中点时,求
的中点时,求 与平面
与平面 所成的角的正弦值;
所成的角的正弦值;
(Ⅲ)是否存在点 使得二面角
使得二面角 为直二面角?若存在,请确定点E的位置;若不存在,请说明理由.
为直二面角?若存在,请确定点E的位置;若不存在,请说明理由.
(1)只需证PA⊥BC,AC⊥BC即可;(2)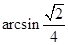 ;(3)故存在点E使得二面角
;(3)故存在点E使得二面角 是直二面角,此时
是直二面角,此时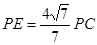 。
。
解析试题分析:(Ⅰ)∵PA⊥底面ABC,∴PA⊥BC.
又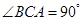 ,∴AC⊥BC.
,∴AC⊥BC.
∴BC⊥平面PAC. 4分
(Ⅱ)∵D为PB的中点,DE//BC,
∴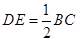 ,
,
又由(Ⅰ)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵PA⊥底面ABC,∴PA⊥AB,又PA=AB,
∴△ABP为等腰直角三角形,∴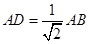 ,
,
∴在Rt△ABC中, ,∴
,∴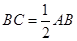 .
.
∴在Rt△ADE中,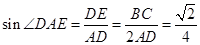 ,
,
∴ 与平面
与平面 所成的角的大小
所成的角的大小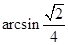 . 9分
. 9分
(Ⅲ)∵DE//BC,又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,
又∵AE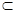 平面PAC,PE
平面PAC,PE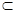 平面PAC,∴DE⊥AE,DE⊥PE,
平面PAC,∴DE⊥AE,DE⊥PE,
∴∠AEP为二面角 的平面角,
的平面角,
∵PA⊥底面ABC,∴PA⊥AC,∴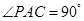
∴在棱PC上存在一点E,使得AE⊥PC,这时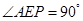 ,
,
故存在点E使得二面角 是直二面角.
是直二面角.
此时 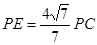 14分
14分
考点:线面垂直的判定定理;线面垂直的性质定理;线面角;二面角。
点评:本题主要考查了直线与平面所成的角以及二面角,属立体几何中的常考题型,较难.充分考查了学生的逻辑推理能力,空间想象力,以及识图能力。

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
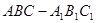 中, AC=4,CB=2,AA1=2,
中, AC=4,CB=2,AA1=2,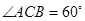 ,E、F分别是
,E、F分别是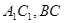 的中点。
的中点。
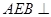 平面
平面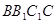 ;
;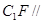 平面ABE;
平面ABE; 的体积。
的体积。 中,
中, ∥
∥ ,
, ,
, ,
, ⊥
⊥ ,
, ⊥
⊥ 为
为 的中点.
的中点.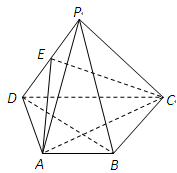
 ∥平面
∥平面 ;
; .
.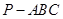 中,
中,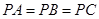 ,
,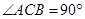 ,
,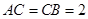 .
. 
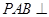 平面
平面 ;
;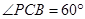 时,求三棱锥
时,求三棱锥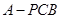 的体积.
的体积. 平面CC1D1D,且PC=PD=
平面CC1D1D,且PC=PD= .
.
 平面PBC;
平面PBC; ,当a为何值时,PC//平面
,当a为何值时,PC//平面 .
. ,
,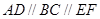 ,
,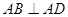 ,
,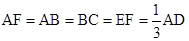
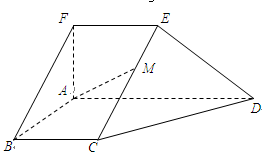
 ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由. 的菱形
的菱形 中,
中, ,
, 面
面 ,
, 、
、 分别是
分别是 和
和 的中点.
的中点.
 面
面 ;
;  ⊥平面
⊥平面 ;
; 与平面
与平面 为圆
为圆 的直径,点
的直径,点 、
、 在圆
在圆 ,矩形
,矩形 所在的平面与圆
所在的平面与圆 ,
, .
.
 平面
平面 ;
;  的长为何值时,平面
的长为何值时,平面 与平面
与平面 所成的锐二面角的大小为
所成的锐二面角的大小为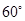 ?
?