题目内容
12.已知集合A={x|x2-x-2≤0},B={y|y=2x,x∈A},则A∩B=( )| A. | [-1,2] | B. | [-1,4] | C. | [$\frac{1}{2}$,4] | D. | [$\frac{1}{2}$,2] |
分析 求出A中不等式的解集确定出A,根据A及指数函数的性质求出B中y的范围,进而确定出B,找出两集合的交集即可.
解答 解:由A中不等式变形得:(x-2)(x+1)≤0,
解得:-1≤x≤2,即A=[-1,2],
由B中y=2x>0,x∈A,得到B=[$\frac{1}{2}$,4),
则A∩B=[$\frac{1}{2}$,2],
故选:D.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.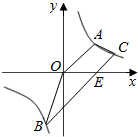 如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),C点的纵坐标为1.
如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),C点的纵坐标为1.
(1)求反比例函数的解析式;
(2)求四边形AOEC的面积.
 如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),C点的纵坐标为1.
如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),C点的纵坐标为1.(1)求反比例函数的解析式;
(2)求四边形AOEC的面积.
1.如果圆(x+3)2+(y-1)2=1关于直线l:mx+4y-1=0对称,则直线l的斜率为( )
| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |

 如图l是东西走向的一水管,在水管北侧有两个半径都是10m的圆形蓄水池A,B(A,B分别为蓄水池的圆心),经测量,点A,B到水管l的距离分别为55m和25m,AB=50m.以l所在直线为x轴,过点A且与l垂直的直线为y轴,建立如图所示的直角坐标系(O为坐标原点).
如图l是东西走向的一水管,在水管北侧有两个半径都是10m的圆形蓄水池A,B(A,B分别为蓄水池的圆心),经测量,点A,B到水管l的距离分别为55m和25m,AB=50m.以l所在直线为x轴,过点A且与l垂直的直线为y轴,建立如图所示的直角坐标系(O为坐标原点).