题目内容
10.若$\vec a$,$\vec b$是两个非零的平面向量,则“$|{\vec a}|=|{\vec b}|$”是“$({\vec a+\vec b})•({\vec a-\vec b})=0$”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义进行判断即可.
解答 解:若$({\vec a+\vec b})•({\vec a-\vec b})=0$,则${\overrightarrow{a}}^{2}={\overrightarrow{b}}^{2}$,即$|{\vec a}|=|{\vec b}|$,
则“$|{\vec a}|=|{\vec b}|$”是“$({\vec a+\vec b})•({\vec a-\vec b})=0$”的充要条件,
故选:C
点评 本题主要考查充分条件和必要条件的判断,利用向量数量积的运算和性质是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.执行如图所示的程序框图,则输出的结果为( )


| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
15.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A. | y=|x+2| | B. | y=|x|+2 | C. | y=-x2+2 | D. | $y={({\frac{1}{2}})^{|x|}}$ |
2.已知函数$f(x)=\left\{\begin{array}{l}{log_2}x,x≥1\\ f({2x}),0<x<1.\end{array}\right.$则$f[{{{({\frac{1}{2}})}^{\frac{1}{2}}}}]$=( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |
19. 下表记录了某学生进入高三以来各次数学考试的成绩
下表记录了某学生进入高三以来各次数学考试的成绩
将第1次到第12次的考试成绩依次记为a1,a2,…,a12.图2是统计上表中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是7.
 下表记录了某学生进入高三以来各次数学考试的成绩
下表记录了某学生进入高三以来各次数学考试的成绩| 考试第次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 成绩(分) | 65 | 78 | 85 | 87 | 88 | 99 | 90 | 94 | 93 | 102 | 105 | 116 |
 在三棱锥P-ABC中,PA⊥底面ABC,D为BC的中点,PB=PC=$\sqrt{26}$,cos∠BPC=$\frac{5}{13}$,在△PAD中,过A作AM⊥PD于M.
在三棱锥P-ABC中,PA⊥底面ABC,D为BC的中点,PB=PC=$\sqrt{26}$,cos∠BPC=$\frac{5}{13}$,在△PAD中,过A作AM⊥PD于M.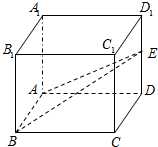 在正方体ABCD-A1B1C1D1中,E是棱DD1的中点,四棱锥E-ABCD的体积为$\frac{4}{3}$,求异面直线BE与B1A1所成的角的大小(结果用反三角函数值表示).
在正方体ABCD-A1B1C1D1中,E是棱DD1的中点,四棱锥E-ABCD的体积为$\frac{4}{3}$,求异面直线BE与B1A1所成的角的大小(结果用反三角函数值表示).