题目内容
 已知曲线C:x2-y|y|=1(|x|≤4).
已知曲线C:x2-y|y|=1(|x|≤4).(1)画出曲线C的图象,
(2)(文)若直线l:y=x+m与曲线C有两个公共点,求m的取值范围;
(理)若直线l:y=kx-1与曲线C有两个公共点,求k的取值范围;
(3)若P(0,p)(p>0),Q为曲线C上的点,求|PQ|的最小值.
分析:(1)去掉绝对值,将曲线化为两段曲线,分别画出这两段曲线即可
(2)理,直线y=kx-1过定点(0,-1),先讨论y≤0时有两个公共点时k的取值范围,再讨论y>0时有一个公共点时k的取值范围,最后将两个范围合并即可
文,直线y=x+m的斜率为1,先讨论y≤0时有两个公共点时m的取值范围,再讨论y>0时有一个公共点时m的取值范围,最后将两个范围合并即可
(3)将|PQ|表示为关于变量y的函数,先讨论y≤0时函数的最小值,再讨论y>0时函数的最小值,最后将两个结果比较,取较小的作为|PQ|的最小值即可.
(2)理,直线y=kx-1过定点(0,-1),先讨论y≤0时有两个公共点时k的取值范围,再讨论y>0时有一个公共点时k的取值范围,最后将两个范围合并即可
文,直线y=x+m的斜率为1,先讨论y≤0时有两个公共点时m的取值范围,再讨论y>0时有一个公共点时m的取值范围,最后将两个范围合并即可
(3)将|PQ|表示为关于变量y的函数,先讨论y≤0时函数的最小值,再讨论y>0时函数的最小值,最后将两个结果比较,取较小的作为|PQ|的最小值即可.
解答:解:(1)当y>0时,曲线为x2-y2=1
当y≤0时,曲线为x2+y2=1
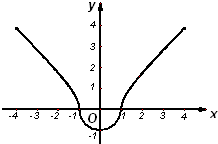 画出曲线C的图象如图
画出曲线C的图象如图
理(2)若l:y=kx-1与x2+y2=1(y≤0)有两个公共点,
则k∈[-1,0)∪(0,1]
若l:y=kx-1与x2-y2=1(y>0)恰有一个公共点时直线l:y=kx-1与曲线C也有两个公共点,
所以由
⇒(1-k2)x2+2kx-2=0,
∴|k|>1,△=4k2+8(1-k2)=8-4k2=0,
解得 k=±
.
∴k的取值范围是{-
}∪∈[-1,0)∪(0,1]∪{
}
文(2)若l:y=x+m与x2+y2=1(y≤0)有两个公共点,
则d=
∈[
,1],解得 m∈(-
,-1]
若l:y=x+m与x2+y2=1(y≤0)和x2-y2=1(y>0)各有一个公共点,
则由图象知,m∈(-1,0)
∴m的取值范围是(-
,0)
(3)当y≤0时,|PQ|2=x2+(y-p)2=1-2py+p2
由-1≤y≤0得,当y=0时| PQ |min=
当y>0时,|PQ|2=x2+(y-p)2=2y2-2py+p2+1=2( y-
)2+
p2+1
当y=
p 时| PQ |min=
由于
>
∴|PQ|的最小值是
当y≤0时,曲线为x2+y2=1
 画出曲线C的图象如图
画出曲线C的图象如图理(2)若l:y=kx-1与x2+y2=1(y≤0)有两个公共点,
则k∈[-1,0)∪(0,1]
若l:y=kx-1与x2-y2=1(y>0)恰有一个公共点时直线l:y=kx-1与曲线C也有两个公共点,
所以由
|
∴|k|>1,△=4k2+8(1-k2)=8-4k2=0,
解得 k=±
| 2 |
∴k的取值范围是{-
| 2 |
| 2 |
文(2)若l:y=x+m与x2+y2=1(y≤0)有两个公共点,
则d=
| |m| | ||
|
| ||
| 2 |
| 2 |
若l:y=x+m与x2+y2=1(y≤0)和x2-y2=1(y>0)各有一个公共点,
则由图象知,m∈(-1,0)
∴m的取值范围是(-
| 2 |
(3)当y≤0时,|PQ|2=x2+(y-p)2=1-2py+p2
由-1≤y≤0得,当y=0时| PQ |min=
| 1+p2 |
当y>0时,|PQ|2=x2+(y-p)2=2y2-2py+p2+1=2( y-
| p |
| 2 |
| 1 |
| 2 |
当y=
| 1 |
| 2 |
1+
|
由于
| 1+p2 |
1+
|
∴|PQ|的最小值是
1+
|
点评:本题综合考查了直线与圆,直线与双曲线的关系,解题时要善于使用数形结合的思想方法,善于分类讨论,做到不重不漏,运算要认真准确,才能顺利解题

练习册系列答案
相关题目
 (2006•浦东新区模拟)已知曲线C:x2-y|y|=1(|x|≤4).
(2006•浦东新区模拟)已知曲线C:x2-y|y|=1(|x|≤4).