题目内容
已知曲线C:x2-y|y|=1.
(1)画出曲线C的图象,
(2)若直线l:y=x+m与曲线C有两个公共点,求m的取值范围;
(3)若过点P(0,2)的直线与曲线C在x轴上方的部分交于不同的两点M,N,求t=
•
+
•
的范围.
(1)画出曲线C的图象,
(2)若直线l:y=x+m与曲线C有两个公共点,求m的取值范围;
(3)若过点P(0,2)的直线与曲线C在x轴上方的部分交于不同的两点M,N,求t=
| OM |
| OP |
| OM |
| PN |
分析:(1)去掉绝对值,将曲线化为两段曲线,分别画出这两段曲线即可;
(2)直线y=x+m的斜率为1,先讨论y≤0时有两个公共点时m的取值范围,再讨论y>0时有一个公共点时m的取值范围,最后将两个范围合并即可;
(3)设出直线方程方程,与曲线方程联立,利用韦达定理及向量知识,利用k的范围,即可确定t的范围.
(2)直线y=x+m的斜率为1,先讨论y≤0时有两个公共点时m的取值范围,再讨论y>0时有一个公共点时m的取值范围,最后将两个范围合并即可;
(3)设出直线方程方程,与曲线方程联立,利用韦达定理及向量知识,利用k的范围,即可确定t的范围.
解答: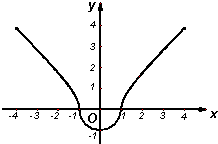 解:(1)当y>0时,x2-y2=1(2分)
解:(1)当y>0时,x2-y2=1(2分)
当y≤0时x2+y2=1(2分)
曲线C的图象,如图所示…(计4分)
(2)若l:y=x+m与x2+y2=1(y≤0)有两个公共
点,则d=
∈[
,1),解得m∈(-
,-1] …(6分)
若l:y=x+m与x2+y2=1(y≤0)和x2-y2=1
(y>0)各有一个公共点,
则由图象知,m∈(-1,0)…(8分)
∴m的取值范围是(-
,0) …(9分)
(3)设过点P(0,2)的直线为y=kx+2
则由图象知,k∈(-1,1),…(10分)
设M,N的坐标为M(x1,y1),N(x2,y2),则由
得(1-k2)x2-4kx-5=0,
∴x1+x2=
,x1x2=
…(12分)
∴t=
•
+
•
=
•(
+
)=
•
=x1x2+y1y2=x1x2+(kx1+2)(kx2+2)=(1+k2)x1x2+2k(x1+x2)+4
=(1+k2)•
+2k•
+4=
+4=1+
∵k∈(-1,1),∴0≤k2<1,∴-1≤k2-1<0,∴
≤-1
∴1+
≤-1,∴t≤-1…(14分)
 解:(1)当y>0时,x2-y2=1(2分)
解:(1)当y>0时,x2-y2=1(2分)当y≤0时x2+y2=1(2分)
曲线C的图象,如图所示…(计4分)
(2)若l:y=x+m与x2+y2=1(y≤0)有两个公共
点,则d=
| |m| | ||
|
| ||
| 2 |
| 2 |
若l:y=x+m与x2+y2=1(y≤0)和x2-y2=1
(y>0)各有一个公共点,
则由图象知,m∈(-1,0)…(8分)
∴m的取值范围是(-
| 2 |
(3)设过点P(0,2)的直线为y=kx+2
则由图象知,k∈(-1,1),…(10分)
设M,N的坐标为M(x1,y1),N(x2,y2),则由
|
得(1-k2)x2-4kx-5=0,
∴x1+x2=
| 4k |
| 1-k2 |
| -5 |
| 1-k2 |
∴t=
| OM |
| OP |
| OM |
| PN |
| OM |
| OP |
| PN |
| OM |
| ON |
=x1x2+y1y2=x1x2+(kx1+2)(kx2+2)=(1+k2)x1x2+2k(x1+x2)+4
=(1+k2)•
| -5 |
| 1-k2 |
| 4k |
| 1-k2 |
| 3k2-5 |
| 1-k2 |
| 2 |
| k2-1 |
∵k∈(-1,1),∴0≤k2<1,∴-1≤k2-1<0,∴
| 1 |
| k2-1 |
∴1+
| 2 |
| k2-1 |
点评:本题综合考查了直线与圆,直线与双曲线的关系,解题时要善于使用数形结合的思想方法,善于分类讨论,做到不重不漏,属于中档题.

练习册系列答案
相关题目
 (2006•浦东新区模拟)已知曲线C:x2-y|y|=1(|x|≤4).
(2006•浦东新区模拟)已知曲线C:x2-y|y|=1(|x|≤4). 已知曲线C:x2-y|y|=1(|x|≤4).
已知曲线C:x2-y|y|=1(|x|≤4).