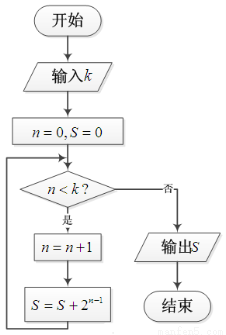
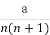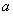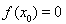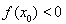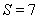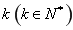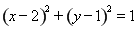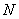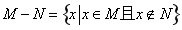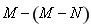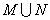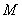题目内容
已知等差数列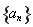 的首项为
的首项为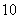 ,公差为
,公差为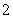 ,数列
,数列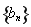 满足
满足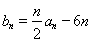 ,
,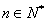 .
.
(1)求数列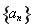 与
与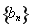 的通项公式;
的通项公式;
(2)记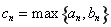 ,求数列
,求数列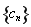 的前
的前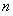 项和
项和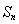 .
.
(注: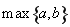 表示
表示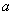 与
与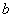 的最大值.)
的最大值.)
(1)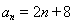 ,
,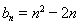 ;(2)
;(2)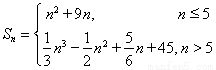 .
.
【解析】
试题分析:(1)利用等差数列的通项公式求出数列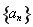 的通项公式,再将数列
的通项公式,再将数列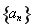 的通项公式代入
的通项公式代入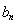 的表达式即可求出数列
的表达式即可求出数列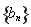 的通项公式;(2)利用作差法比较
的通项公式;(2)利用作差法比较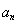 与
与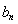 的大小,然后利用定义求出数列
的大小,然后利用定义求出数列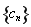 的通项公式(利用分段表达式进行表示),然后对
的通项公式(利用分段表达式进行表示),然后对 的取值分段求出
的取值分段求出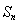 .
.
试题解析:(1)由于数列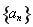 是以
是以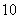 为首项,以
为首项,以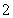 为公差的等差数列,
为公差的等差数列,
因此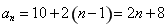 ,
,
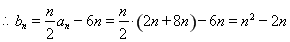 ;
;
(2)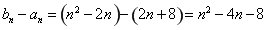 ,
,
令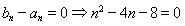 ,解得
,解得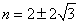 ,
,
因此当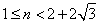 时,
时,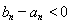 ,即
,即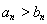 ,
,
因此当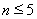 且
且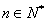 时,
时,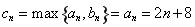 ,
,
当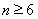 且
且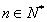 时,
时,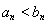 ,
,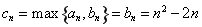 ,
,
当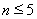 且
且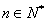
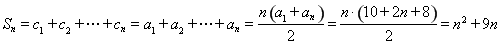 ,
,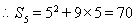 ,
,
当 且
且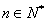 时,
时,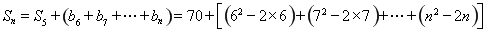
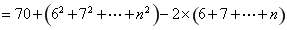
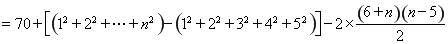
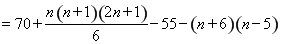
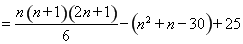
 ,
,
所以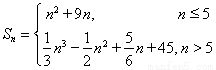 .
.
考点:1.等差数列的通项公式;2.利用作差法比较大小;3.分段求和

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目