题目内容
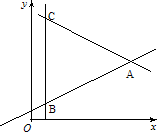 给出平面区域如图所示,其中A(5,3),B(1,1),C(1,5),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )
给出平面区域如图所示,其中A(5,3),B(1,1),C(1,5),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )A、
| ||
B、
| ||
| C、2 | ||
D、
|
分析:给出平面区域如图所示,其中A(5,3),B(1,1),C(1,5),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为
解答:解:∵目标函数P=ax+y,
∴y=-ax+P.
故目标函数值Z是直线族y=-ax+P的截距,
当直线族y=-ax+P的斜率与边界AC的斜率相等时,
目标函数z=ax+y取得最大值的最优解有无数多个,
此时,-a=
=
,
即a=
,
故选B.
∴y=-ax+P.
故目标函数值Z是直线族y=-ax+P的截距,
当直线族y=-ax+P的斜率与边界AC的斜率相等时,
目标函数z=ax+y取得最大值的最优解有无数多个,
此时,-a=
| 3-5 |
| 5-1 |
| 1 |
| 2 |
即a=
| 1 |
| 2 |
故选B.
点评:目标函数的最优解有无数多个,处理方法一般是:①将目标函数的解析式进行变形,化成斜截式②分析Z与截距的关系,是符号相同,还是相反③根据分析结果,结合图形做出结论④根据斜率相等求出参数.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
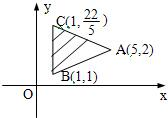 给出平面区域如图所示,若使目标函数Z=ax+y (a>0),取得最大值的最优解有无数个,则a值为
给出平面区域如图所示,若使目标函数Z=ax+y (a>0),取得最大值的最优解有无数个,则a值为
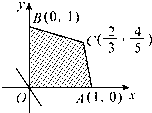 (2007•湛江二模)给出平面区域如图所示,若点C是目标函数z=ax-y取最小值的唯一最优解,则实数a的取值范围是
(2007•湛江二模)给出平面区域如图所示,若点C是目标函数z=ax-y取最小值的唯一最优解,则实数a的取值范围是

 取得最大值的最优解有无穷多个,则
取得最大值的最优解有无穷多个,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
