题目内容
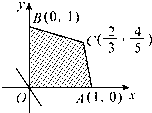（2007•湛江二模）给出平面区域如图所示，若点C是目标函数z=ax-y取最小值的唯一最优解，则实数a的取值范围是(-
， -
)
| 12 |
| 5 |
| 3 |
| 10 |
(-
， -
)
．| 12 |
| 5 |
| 3 |
| 10 |
分析：要满足题意需目标直线y=ax-z的斜率a介于两直线的斜率之间，分别求得斜率可得．
解答：解：由题意可得直线BC的斜率k=
=-
，
直线CA的斜率k′=
=-
，
要使点C是目标函数z=ax-y取最小值的唯一最优解，
需使目标直线y=ax-z的斜率a介于两直线的斜率之间，
故可得a的取值范围为（-
，-
），
故答案为：（-
，-
）
1-
| ||
0-
|
| 3 |
| 10 |
直线CA的斜率k′=
0-
| ||
1-
|
| 12 |
| 5 |
要使点C是目标函数z=ax-y取最小值的唯一最优解，
需使目标直线y=ax-z的斜率a介于两直线的斜率之间，
故可得a的取值范围为（-
| 12 |
| 5 |
| 3 |
| 10 |
故答案为：（-
| 12 |
| 5 |
| 3 |
| 10 |
点评：本题考查简单的线性规划，数形结合是解决问题的关键，属中档题．
练习册系列答案
相关题目
（2007•湛江二模）已知A、B是两个集合，它们的关系如图所示，则下列式子正确的是（ ）