题目内容
一袋中装有分别标记着数字1、2、3、4的4个球,若从这只袋中每次取出1个球,取出后放回,连续取三次,设取出的球中数字最大的数为ξ.(1)求ξ=3时的概率;(2)求ξ的概率分布列及数学期望.分析:(1)ξ=3表示取出的三个球中数字最大者为3,三次取球均出现数字为3的概率p1=(
)3=
,三次取球中有2次出现数字为3的概率p2=
(
)2 (
)=
,三次取球中有1出现数字为3的概率p3=
(
)(
)2=
,由此能求出p(ξ=3)..
(2)在ξ=k时,利用(1)的原理知p(ξ=k)=(
)3+
(
)2(
) +
(
) (
)2=
,k=1,2,3,4.由此能求出ξ的概率分布列及数学期望.
| 1 |
| 4 |
| 1 |
| 64 |
| C | 2 3 |
| 1 |
| 4 |
| 2 |
| 4 |
| 6 |
| 64 |
| C | 1 3 |
| 1 |
| 4 |
| 2 |
| 4 |
| 12 |
| 64 |
(2)在ξ=k时,利用(1)的原理知p(ξ=k)=(
| 1 |
| 4 |
| C | 2 3 |
| 1 |
| 4 |
| k-1 |
| 4 |
| C | 1 3 |
| 1 |
| 4 |
| k-1 |
| 4 |
| 3k2-3k+1 |
| 64 |
解答:解:(1)ξ=3表示取出的三个球中数字最大者为3,
①三次取球均出现数字为3的概率p1=(
)3=
,
②三次取球中有2次出现数字为3的概率p2=
(
)2 (
)=
,
③三次取球中有1出现数字为3的概率p3=
(
)(
)2=
,
∴p(ξ=3)=p1+p2+p3=
.
(2)在ξ=k时,利用(1)的原理知:
p(ξ=k)=(
)3+
(
)2(
) +
(
) (
)2=
,k=1,2,3,4.
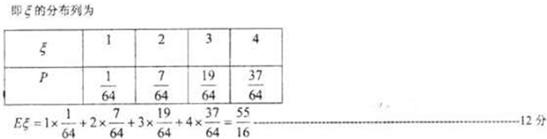
①三次取球均出现数字为3的概率p1=(
| 1 |
| 4 |
| 1 |
| 64 |
②三次取球中有2次出现数字为3的概率p2=
| C | 2 3 |
| 1 |
| 4 |
| 2 |
| 4 |
| 6 |
| 64 |
③三次取球中有1出现数字为3的概率p3=
| C | 1 3 |
| 1 |
| 4 |
| 2 |
| 4 |
| 12 |
| 64 |
∴p(ξ=3)=p1+p2+p3=
| 19 |
| 64 |
(2)在ξ=k时,利用(1)的原理知:
p(ξ=k)=(
| 1 |
| 4 |
| C | 2 3 |
| 1 |
| 4 |
| k-1 |
| 4 |
| C | 1 3 |
| 1 |
| 4 |
| k-1 |
| 4 |
| 3k2-3k+1 |
| 64 |

点评:本题考查概率的性质和应用,解题时要认真审题,仔细解答,注意离散型随机变量概率分布列的求法.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 ,设
,设 ,则
,则 .
.