题目内容
函数f(x)=
与函数g（x）=2x+a仅有一个实根，则实数a的取值范围为
|
a＞4或a＜3
a＞4或a＜3
．分析：要求满足条件关于x的方程f（x）+x-a=0有且仅有两个实根时，实数a的取值范围，我们可以转化求函数y=f（x）与函数y=-x+a的图象，有且仅有两个交点时实数a的取值范围．
解答：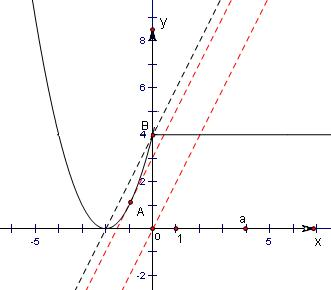
解：函数f(x)=
的图象如图所示，
当a=3时，函数y=f（x）与函数y=2x+a的图象相切，只有一个交点，
当a=4时，直线y=2x+a过点B（0，4），此时函数y=f（x）与函数y=2x+a的图象相切，有2个交点，
由图可知，当a＞4或a＜3时，函数y=f（x）与函数y=2x+a的图象有且仅有两个交点，即当a＞4或a＜3时，g（x）=2x+a仅有一个实根，
故答案为：a＞4或a＜3．
解：函数f(x)=
|
当a=3时，函数y=f（x）与函数y=2x+a的图象相切，只有一个交点，
当a=4时，直线y=2x+a过点B（0，4），此时函数y=f（x）与函数y=2x+a的图象相切，有2个交点，
由图可知，当a＞4或a＜3时，函数y=f（x）与函数y=2x+a的图象有且仅有两个交点，即当a＞4或a＜3时，g（x）=2x+a仅有一个实根，
故答案为：a＞4或a＜3．
点评：本题考查的知识点是根的存在性及根的个数判断，根据方程的根即为对应函数零点，将本题转化为求函数零点个数，进而利用图象法进行解答是解答本题的关键．
练习册系列答案
相关题目
已知函数f(x)=
若f（2-a2）＞f（a），则实数a的取值范围是（ ）
|
| A、（-∞，-1）∪（2，+∞） |
| B、（-1，2） |
| C、（-2，1） |
| D、（-∞，-2）∪（1，+∞） |