题目内容
(12分)在 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是 ,已知
,已知 ,
, ,
,
(1)求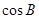 的值;
的值;
(2)若 ,求
,求 的值.
的值.
(1)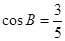 ;(2)
;(2)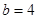 .
.
解析试题分析:(1) ,
,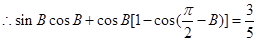 ,
,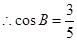 .
.
(2)因为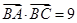 ,所以
,所以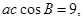
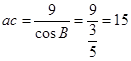 ,
,
所以 ,
,
所以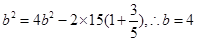 .
.
考点:平面向量的数量积的坐标表示,余弦定理.
点评:根据两个向量的数量积的坐标表示就是横坐标积与纵坐标积的和,得到关于B的方程,可求得cosB的值.第(2)问关键知道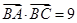 就是
就是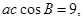 从而得到ac的值,再结合余弦定理的变形形式可得
从而得到ac的值,再结合余弦定理的变形形式可得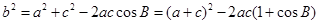 ,从而求出得b的值.
,从而求出得b的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的最小正周期为
的最小正周期为 ,最小值为
,最小值为 ,图象过点
,图象过点 ,(1)求
,(1)求 的解析式;(2)求满足
的解析式;(2)求满足 且
且
 的
的 的集合.
的集合. 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 的前
的前 项和
项和
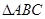 中,
中,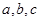 分别是角
分别是角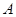 ,
,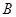 ,
, 的对边,且
的对边,且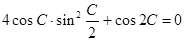 .
.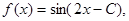 求
求 的单调增区间;
的单调增区间;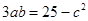 ,求
,求 中,
中,  、
、 、
、 分别为角
分别为角 、
、 、
、 所对的边,且角
所对的边,且角
 的值;
的值; ,
, 时,求
时,求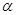 是第三角限角,化简
是第三角限角,化简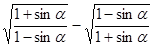 .
. ,求
,求 的值.
的值. 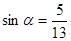 ,求
,求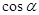 ,
,
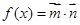 ,其中
,其中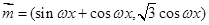 ,
,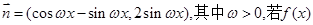 相邻两对称轴间的距离不小于
相邻两对称轴间的距离不小于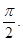
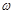 的取值范围;
的取值范围; 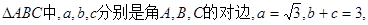
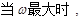
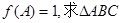 的面积.
的面积.