题目内容
(本题18分)
已知:正数数列 的通项公式
的通项公式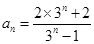

(1)求数列 的最大项;[来源:Zxxk.Com]
的最大项;[来源:Zxxk.Com]
(2)设 ,确定实常数
,确定实常数 ,使得
,使得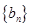 为等比数列;
为等比数列;
(3)(理)数列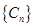 ,满足
,满足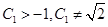 ,
,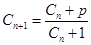 ,其中
,其中 为第(2)小题中确定的正常数,求证:对任意
为第(2)小题中确定的正常数,求证:对任意 ,有
,有 且
且 或
或 且
且 成立.
成立.
(文)设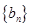 是满足第(2)小题的等比数列,求使不等式
是满足第(2)小题的等比数列,求使不等式 成立的最小正整数
成立的最小正整数 .
.
【答案】
(1)4(2)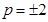 (3)略
(3)略
【解析】(1) ,随n的增大而减小,
,随n的增大而减小,
∴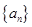 中的最大项为
中的最大项为 (2’)
(2’)
(2)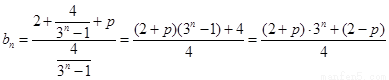 (4’)
(4’)
 为等比数列
为等比数列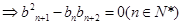


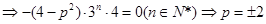
反之当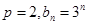 时,
时, 为等比数列;
为等比数列;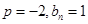 时,
时, 为等比数列
为等比数列
∴当且仅当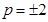 时,
时,  为等比数列(8’)
为等比数列(8’)
(3)(理)按题意 [来源:学+科+网]
[来源:学+科+网]
∵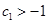 ,
, ,进而当
,进而当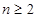 时,
时, (10’)
(10’)
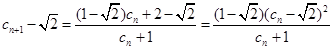
∵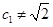 ,∴由数学归纳法,对
,∴由数学归纳法,对 ,且
,且
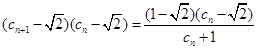
 (15’)
(15’)
特别有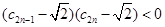

∴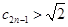 且
且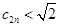 或
或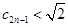 且
且 (18’)
(18’)
(文)若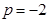 ,则
,则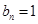

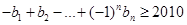 的
的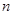 不存在(11’)
不存在(11’)
若 ,则
,则

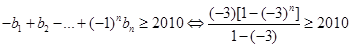
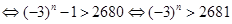 (16’)
(16’)
∴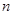 为偶数 ∵
为偶数 ∵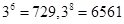
∴当 时,
时,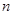 的最小值为8;当
的最小值为8;当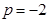 时,满足条件的
时,满足条件的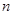 不存在(18’)
不存在(18’)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
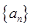 :
: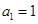 、
、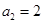 、
、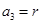 且
且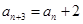 (
(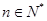 ),与数列
),与数列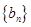 :
: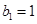 、
、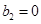 、
、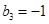 、
、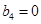 且
且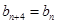 (
(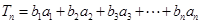 .
.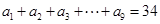 ,求
,求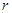 的值;
的值;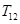 的值,并求证当
的值,并求证当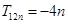 ;
;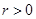 ,且存在正整数
,且存在正整数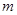 ,使得在
,使得在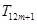 ,
,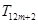 ,
, ,
,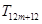 中有4项为100.求
中有4项为100.求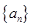 :
: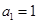 、
、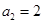 、
、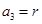 且
且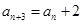 (
(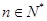 ),与数列
),与数列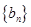 :
: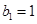 、
、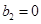 、
、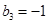 、
、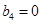 且
且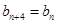 (
(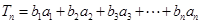 .
. ,求
,求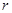 的值;
的值;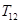 的值,并求证当
的值,并求证当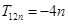 ;
;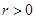 ,且存在正整数
,且存在正整数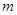 ,使得在
,使得在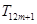 ,
,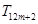 ,
, ,
,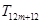 中有4项为100。求
中有4项为100。求