题目内容
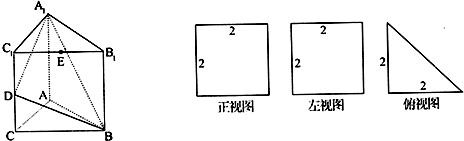 直三棱柱A1B1C1-ABC的三视图如图所示,D、E分别为棱CC1和B1C1的中点.
直三棱柱A1B1C1-ABC的三视图如图所示,D、E分别为棱CC1和B1C1的中点.(1)求异面直线A1D与AB所成角的余弦值;
(2)求点C到平面A1BD的距离;
(3)在AC上是否存在一点F,使EF⊥平面A1BD,若存在确定其位置,若不存在,说明理由.
分析:(1)建立空间直角坐标系,分别求出两条直线所在的向量,进而利用向量的有关运算求出空间向量的夹角,再转化为两条异面直线的夹角.
(2)求出平面的法向量以及平面的一条斜线所在的向量,再求出斜线所在的向量在法向量上射影,进而得到答案.
(3)设F(x,0,0),由E(0,1,2),可求出向量
,则
为平面A1BD的一个法向量,由此构造方程,求出x值,即可得到F点的位置.
(2)求出平面的法向量以及平面的一条斜线所在的向量,再求出斜线所在的向量在法向量上射影,进而得到答案.
(3)设F(x,0,0),由E(0,1,2),可求出向量
| EF |
| EF |
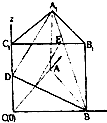
解答:解:(1)如图建立空间直角坐标系,则B(2,0,0),D(0,0,1),A1(0,2,2),A(0,2,0),
所以
=(0,-2,-1),
=(2,-2,0),
所以cos<A1D,AB>=|
|=
.
所以异面直线A1D与AB所成角的余弦值为
.
(2)由(1)可得:
=(0,-2,-1)
(-2,0,1),
设平面A1DB的法向量为
=(x,y,z),
则
,取x=-1
所以可得:
=(-1,1,-2),
又因为
=(0,0,1),
所以cos<n1,
>=
=
=
,
所以d=|
|•
=
.
所以点C到平面A1BD的距离
.
(3)存在F为AC的中点,使EF⊥平面A1BD
设F(0,y,0),由E(1,0,2)得
=(-1,y,-2)
若EF⊥平面A1BD,则
∥
由
=(-1,1,-2)得y=1,
∴F为AC的中点
∴存在F为AC的中点,使EF⊥平面A1BD
所以
| A1D |
| AB |
所以cos<A1D,AB>=|
| ||||
|
|
| ||
| 5 |

所以异面直线A1D与AB所成角的余弦值为
| ||
| 5 |
(2)由(1)可得:
| A1D |
| ,BD |
设平面A1DB的法向量为
| n1 |
则
|
所以可得:
| n1 |
又因为
| CD |
所以cos<n1,
| CD |
n1•
| ||
|n1|•|
|
| 2 | ||
|
2
| ||
| 6 |
所以d=|
| CD |
2
| ||
| 6 |
2
| ||
| 6 |
所以点C到平面A1BD的距离
2
| ||
| 6 |
(3)存在F为AC的中点,使EF⊥平面A1BD
设F(0,y,0),由E(1,0,2)得
| EF |
若EF⊥平面A1BD,则
| EF |
| n1 |
| n1 |
∴F为AC的中点
∴存在F为AC的中点,使EF⊥平面A1BD
点评:本题考查的知识点是利用空间向量夹角空间夹角与空间距离等问题,并且考查由三视图还原实物图,以及基本运算能力.

练习册系列答案
相关题目
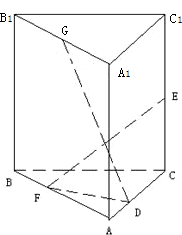 如图,在直三棱柱A1B1C1-ABC中,∠BAC=
如图,在直三棱柱A1B1C1-ABC中,∠BAC=| π |
| 2 |
A、[
| ||||||
B、[
| ||||||
C、[1,
| ||||||
D、[
|
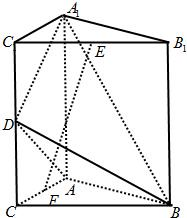 如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.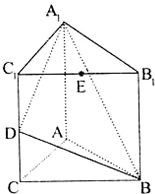 直三棱柱A1B1C1-ABC的三视图如图所示,D、E分别为棱CC1和B1C1的中点.
直三棱柱A1B1C1-ABC的三视图如图所示,D、E分别为棱CC1和B1C1的中点.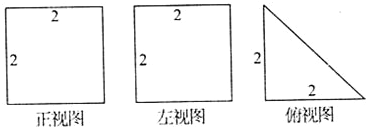
 如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.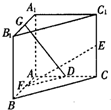 如图,在直三棱柱A1B1C1-ABC中,∠BAC=
如图,在直三棱柱A1B1C1-ABC中,∠BAC=