Question

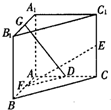如图，在直三棱柱A₁B₁C₁-ABC中，∠BAC=

π

2

，AB=AC=AA₁=2，点G与E分别为线段A₁B₁和C₁C的中点，点D与F分别为线段AC和AB上的动点．若GD⊥EF，则线段DF长度的最小值是

2 5

5

．

Answer 1

分析：建立空间直角坐标系，设出F、D的坐标，求出向量

DG

，

EF

，利用GD⊥EF求得关系式，写出DF的表达式，然后利用二次函数求最值．

解答：解：建立如图所示的空间直角坐标系，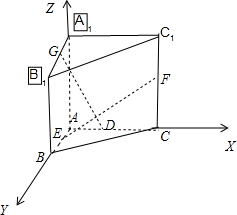
则A（0，0，0），E（0，2，1），
G（1，0，2），F（x，0，0），D（0，y，0）

DG

=（1，-y，2），

EF

=（x，-2，-1）
由于GD⊥EF，
所以   x+2y-2=0
∴|DF|=

x2+y2

=

5y2-8y+4

=

5(y- 4 5 )2+ 4 5

∴当y=

4

5

时，线段DF长度的最小值是 

2 5

5

．
故答案为：

2 5

5

．

点评：本题考查棱柱的结构特征，考查空间想象能力，空间直角坐标系，数量积等知识，是中档题．解决问题的关键在于建立适当的直角坐标系，把问题转化为利用二此函数知识解决．