Question

已知A，B，C为△ABC的三个内角，其所对的边分别为a，b，c，且2cos²＋cos A＝0.

(1)求角A的值；

(2)若a＝2，b＋c＝4，求△ABC的面积．

 

Answer 1

【答案】

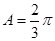（1）；（2）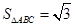

【解析】

试题分析：(1)因为，cosA=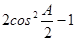

所以，2cos2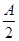＋cos A＝0.可化为，2cosA+1=0

∴cosA=，；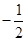

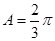(2)根据余弦定理得，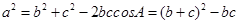

又因为b+c=4，所以12=16－bc，bc=4，。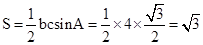

考点：本题主要考查三角函数的和差倍半公式，余弦定理的应用，三角形面积的计算。

点评：中档题，近些年，涉及三角函数、三角形的题目常常出现在高考题中，往往需要综合应用三角公式化简函数，以进一步解题。应用正弦定理、余弦定理求边长、角等，有时运用函数方程思想，问题的解决较为方便。