题目内容
某班从6名班干部（其中男生4人，女生2人）中选3人参加学校学生会的干部竞选．
（1）设所选3人中女生人数为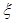
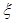，求的分布列
（2）在男生甲被选中的情况下，求女生乙也被选中的概率．
（1）设所选3人中女生人数为
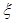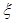，求的分布列 （2）在男生甲被选中的情况下，求女生乙也被选中的概率．
本试题主要考查了分布列和概率的求解运算。第一问中， 先定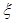的可能取值，然后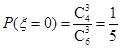
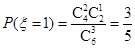
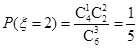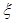得到的分布列
第二问中，是一个条件概率，则在男生甲被选中的情况下，解;设“男生甲被选中”为事件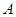
，“女生乙被选中”为事件
，
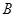则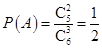
，
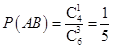，所以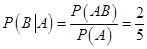
（1）解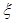：的所有可能取值为0，1，2．…………………………1分
依题意，得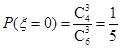 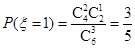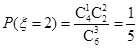， ． ……4分
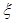∴的分布列为
∴
（2）解;设“男生甲被选中”为事件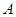，“女生乙被选中”为事件，
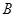则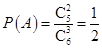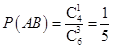，， …………………………………10分
∴．
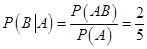故在男生甲被选中的情况下，女生乙也被选中的概率为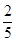
．………………12分
解法2：设“男生甲被选中的情况下，女生乙也被选中”为事件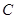
，
从4个男生、2个女生中选3人，男生甲被选中的种数为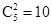
，…………………………8分
男生甲被选中，女生乙也被选中的种数为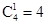
，…………………………10分
∴
．
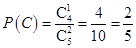故在男生甲被选中的情况下，女生乙也被选中的概率为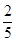．………………12分
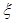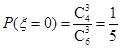
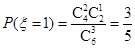
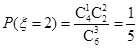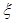的可能取值，然后 得到的分布列第二问中，是一个条件概率，则在男生甲被选中的情况下，解;设“男生甲被选中”为事件
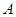，“女生乙被选中”为事件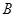，则
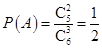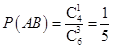，，所以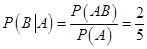（1）解：
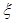的所有可能取值为0，1，2．…………………………1分依题意，得
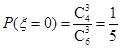
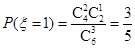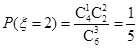， ． ……4分 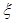| 0 | 1 | 2 | ||
 |  |  |
|
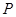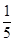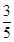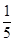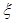的分布列为∴
（2）解;设“男生甲被选中”为事件
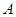，“女生乙被选中”为事件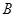，则
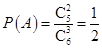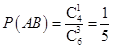，， …………………………………10分∴
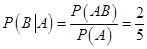．故在男生甲被选中的情况下，女生乙也被选中的概率为
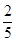．………………12分解法2：设“男生甲被选中的情况下，女生乙也被选中”为事件
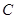，从4个男生、2个女生中选3人，男生甲被选中的种数为
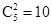，…………………………8分男生甲被选中，女生乙也被选中的种数为
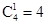，…………………………10分∴
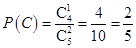．故在男生甲被选中的情况下，女生乙也被选中的概率为
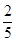．………………12分
练习册系列答案
相关题目
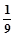(已知甲回答每个问题的正确率相同，并且相互之间没有影响)
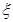（单位：月）服从正态分布
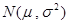，且使用寿命不少于
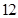个月的概率为
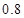，使用寿命不少于
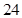个月的概率为
.
；
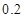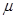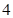支这种新灯管，使用
元，求
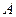和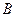
都不发生的概率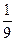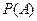为
，
为 。