题目内容
如果函数f(x)同时满足下列条件:①在闭区间[a,b]内连续,②在开区间(a,b)内可导且其导函数为f′(x),那么在区间(a,b)内至少存在一点ξ(a<ξ<b),使得f(b)-f(a)=f′(ξ)(b-a)成立,我们把这一规律称为函数f(x)在区间(a,b)内具有“Lg”性质,并把其中的ξ称为中值.有下列命题:①若函数f(x)在(a,b)具有“Lg”性质,ξ为中值,点A(a,f(a)),B(b,f(b)),则直线AB的斜率为f′(ξ);
②函数y=
2-
|
| 2 |
| ||
| 2 |
③函数f(x)=x3在(-1,2)内具有“Lg”性质,但中值ξ不唯一;
④若定义在[a,b]内的连续函数f(x)对任意的x1、x2∈[a,b],x1<x2,有
| 1 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
其中你认为正确的所有命题序号是
分析:对每一个命题进行逐一判定是否满足函数f(x)在区间(a,b)内具有“Lg”性质,对于①根据导函数的几何意义进行判定,对于②,函数y在(0,2)上连续且可导,代值计算可得两端点连线的斜率存在x=
时的导数值与之相等,对于③,举反例进行判定即可,对于④,只能保证f(x)是上凸函数,不能保证中值一定在中点处进行判定.
| 2 |
解答:解:对于①,根据导函数的几何意义立即可得正确;
对于②,函数y在(0,2)上连续且可导,代值计算可得两端点连线的斜率为-
又y'=
(2-
)-
(-x),当x=
时,y'=-
,故②正确.
对于③,两端点连线斜率为3
而f'(x)=3x2,令3x2=3,x=±1,在(-1,2)内只有一个中值ξ=1,故③错误;
对于④,
[f(x1)+f(x2)]<f(
)只能保证f(x)是上凸函数,不能保证中值一定在中点处.④错误
故答案为:①②
对于②,函数y在(0,2)上连续且可导,代值计算可得两端点连线的斜率为-
| ||
| 2 |
又y'=
| 1 |
| 2 |
| x2 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
对于③,两端点连线斜率为3
而f'(x)=3x2,令3x2=3,x=±1,在(-1,2)内只有一个中值ξ=1,故③错误;
对于④,
| 1 |
| 2 |
| x1+x2 |
| 2 |
故答案为:①②
点评:本题题意比较新颖,主要考查了导数的几何意义,以及函数恒成立问题和直线的斜率,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
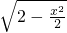 在(0,2)内具有“Lg”性质,且中值ξ=
在(0,2)内具有“Lg”性质,且中值ξ= ,f′(ξ)=-
,f′(ξ)=- ;
; [f(x1)+f(x2)]<f(
[f(x1)+f(x2)]<f( )恒成立,则函数f(x)在(a,b)内具有“Lg”性质,且必有中值ξ=
)恒成立,则函数f(x)在(a,b)内具有“Lg”性质,且必有中值ξ=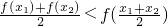 恒成立;
恒成立; 恒成立.
恒成立. 在(0,2)内具有“Lg”性质,且中值ξ=
在(0,2)内具有“Lg”性质,且中值ξ= ,f′(ξ)=-
,f′(ξ)=- ;
; [f(x1)+f(x2)]<f(
[f(x1)+f(x2)]<f( )恒成立,则函数f(x)在(a,b)内具有“Lg”性质,且必有中值ξ=
)恒成立,则函数f(x)在(a,b)内具有“Lg”性质,且必有中值ξ= .
.