题目内容
设函数f(x)=lnx+ax2-(3a+1)x+(2a+1),其中a∈R.
(Ⅰ)如果x=1是函数f(x)的一个极值点,求实数a的值及f(x)的最大值;
(Ⅱ)求实数a的值,使得函数f(x)同时具备如下的两个性质:
①对于任意实数x1,x2∈(0,1)且x1≠x2,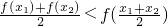 恒成立;
恒成立;
②对于任意实数x1,x2∈(1,+∞)且x1≠x2, 恒成立.
恒成立.
解:(Ⅰ)函数f(x)的定义域是(0,+∞), ,
,
依题意,f'(1)=1+2a-(3a+1)=0,解得a=0.
此时,f(x)=lnx-x+1,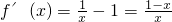 .
.
因为x∈(0,+∞),令f'(x)>0,可得x∈(0,1);令f'(x)<0,可得x∈(1,+∞).
所以,函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
因此,当x=1时,f(x)取得最大值f(1)=0.
(Ⅱ)令
= =
= ,
,
由(Ⅰ)中的结论可知,lnx-x+1<0对任意x∈(0,1)∪(1,+∞)恒成立,即lnx<x-1(*)恒成立.
(ⅰ)如果x1,x2∈(0,1),且x1≠x2,则 .
.
根据(*)可得 ,
, .
.
若f(x)满足性质①,则 恒成立,
恒成立,
于是 对任意x1,x2∈(0,1)且x1≠x2恒成立,所以
对任意x1,x2∈(0,1)且x1≠x2恒成立,所以 .
.
(ⅱ)如果x1,x2∈(1,+∞)且x1≠x2,则 .
.
根据(*)可得 ?
? ,
,
则F(x1,x2)< .若f(x)满足性质②,则
.若f(x)满足性质②,则 恒成立.
恒成立.
于是 对任意x1,x2∈(1,+∞)且x1≠x2恒成立,所以a
对任意x1,x2∈(1,+∞)且x1≠x2恒成立,所以a .
.
综合(ⅰ)(ⅱ)可得,a= .
.
分析:(Ⅰ)先求函数的定义域、导数f′(x),由题意f'(1)=0,解出可得a值,在定义域内解不等式f'(x)>0,f'(x)<0,可得f(x)的单调性,根据单调性可得其最大值;
(Ⅱ)令 =
= ,由(Ⅰ)中的结论可得对任意x∈(0,1)∪(1,+∞),lnx<x-1(*)恒成立.(ⅰ)如果x1,x2∈(0,1),且x1≠x2,则
,由(Ⅰ)中的结论可得对任意x∈(0,1)∪(1,+∞),lnx<x-1(*)恒成立.(ⅰ)如果x1,x2∈(0,1),且x1≠x2,则 .根据(*)可得
.根据(*)可得 ,
, .由性质①转化为恒成立问题,可得a的范围;(ⅱ)如果x1,x2∈(1,+∞)且x1≠x2,则
.由性质①转化为恒成立问题,可得a的范围;(ⅱ)如果x1,x2∈(1,+∞)且x1≠x2,则 .再根据(*)进行放缩,由性质②可得恒成立问题,由此可得a的范围,综合(i)(ii)可得a的范围;
.再根据(*)进行放缩,由性质②可得恒成立问题,由此可得a的范围,综合(i)(ii)可得a的范围;
点评:本题考查利用导数研究函数的极值、最值问题,考查恒成立问题,考查学生综合运用知识分析解决问题的能力,解决(Ⅱ)问的关键是借助(Ⅰ)中的结论得到恰当不等式.
 ,
,依题意,f'(1)=1+2a-(3a+1)=0,解得a=0.
此时,f(x)=lnx-x+1,
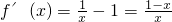 .
.因为x∈(0,+∞),令f'(x)>0,可得x∈(0,1);令f'(x)<0,可得x∈(1,+∞).
所以,函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
因此,当x=1时,f(x)取得最大值f(1)=0.
(Ⅱ)令

=
 =
= ,
,由(Ⅰ)中的结论可知,lnx-x+1<0对任意x∈(0,1)∪(1,+∞)恒成立,即lnx<x-1(*)恒成立.
(ⅰ)如果x1,x2∈(0,1),且x1≠x2,则
 .
.根据(*)可得
 ,
, .
.若f(x)满足性质①,则
 恒成立,
恒成立,于是
 对任意x1,x2∈(0,1)且x1≠x2恒成立,所以
对任意x1,x2∈(0,1)且x1≠x2恒成立,所以 .
.(ⅱ)如果x1,x2∈(1,+∞)且x1≠x2,则
 .
.根据(*)可得
 ?
? ,
,则F(x1,x2)<
 .若f(x)满足性质②,则
.若f(x)满足性质②,则 恒成立.
恒成立.于是
 对任意x1,x2∈(1,+∞)且x1≠x2恒成立,所以a
对任意x1,x2∈(1,+∞)且x1≠x2恒成立,所以a .
.综合(ⅰ)(ⅱ)可得,a=
 .
.分析:(Ⅰ)先求函数的定义域、导数f′(x),由题意f'(1)=0,解出可得a值,在定义域内解不等式f'(x)>0,f'(x)<0,可得f(x)的单调性,根据单调性可得其最大值;
(Ⅱ)令
 =
= ,由(Ⅰ)中的结论可得对任意x∈(0,1)∪(1,+∞),lnx<x-1(*)恒成立.(ⅰ)如果x1,x2∈(0,1),且x1≠x2,则
,由(Ⅰ)中的结论可得对任意x∈(0,1)∪(1,+∞),lnx<x-1(*)恒成立.(ⅰ)如果x1,x2∈(0,1),且x1≠x2,则 .根据(*)可得
.根据(*)可得 ,
, .由性质①转化为恒成立问题,可得a的范围;(ⅱ)如果x1,x2∈(1,+∞)且x1≠x2,则
.由性质①转化为恒成立问题,可得a的范围;(ⅱ)如果x1,x2∈(1,+∞)且x1≠x2,则 .再根据(*)进行放缩,由性质②可得恒成立问题,由此可得a的范围,综合(i)(ii)可得a的范围;
.再根据(*)进行放缩,由性质②可得恒成立问题,由此可得a的范围,综合(i)(ii)可得a的范围;点评:本题考查利用导数研究函数的极值、最值问题,考查恒成立问题,考查学生综合运用知识分析解决问题的能力,解决(Ⅱ)问的关键是借助(Ⅰ)中的结论得到恰当不等式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目