题目内容
函数y=Asin(ωx+φ)(ω>0,|φ|≤ )的部分图象如图所示,则函数的一个表达式为( )
)的部分图象如图所示,则函数的一个表达式为( )

 )的部分图象如图所示,则函数的一个表达式为( )
)的部分图象如图所示,则函数的一个表达式为( )
A.y=-4sin( x+ x+ ) ) |
B.y=4sin( x- x- ) ) |
C.y=-4sin( x- x- ) ) |
D.y=4sin( x+ x+ ) ) |
A
根据正弦函数y=Asin(ωx+φ)(ω>0,|φ|≤ )的图象的性质可得T=2|6-(-2)|=16,故ω=
)的图象的性质可得T=2|6-(-2)|=16,故ω=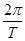 =
= ,又根据图象可知f(6)=0,即Asin(
,又根据图象可知f(6)=0,即Asin( ×6+φ)=0.由于|φ|≤
×6+φ)=0.由于|φ|≤ ,故只能
,故只能 ×6+φ=π,解得φ=
×6+φ=π,解得φ= ,
,
即y=Asin( x+
x+ ),又由f(2)=-4,
),又由f(2)=-4,
即Asin( ×2+
×2+ )=-4,解得A=-4,
)=-4,解得A=-4,
故f(x)=-4sin( x+
x+ ).
).
 )的图象的性质可得T=2|6-(-2)|=16,故ω=
)的图象的性质可得T=2|6-(-2)|=16,故ω=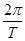 =
= ,又根据图象可知f(6)=0,即Asin(
,又根据图象可知f(6)=0,即Asin( ×6+φ)=0.由于|φ|≤
×6+φ)=0.由于|φ|≤ ,故只能
,故只能 ×6+φ=π,解得φ=
×6+φ=π,解得φ= ,
,即y=Asin(
 x+
x+ ),又由f(2)=-4,
),又由f(2)=-4,即Asin(
 ×2+
×2+ )=-4,解得A=-4,
)=-4,解得A=-4,故f(x)=-4sin(
 x+
x+ ).
).
练习册系列答案
相关题目
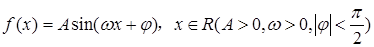 的一段图象如图5所示:将
的一段图象如图5所示:将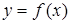 的图像向右平移
的图像向右平移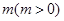 个单位,可得到函数
个单位,可得到函数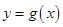 的图象,且图像关于原点对称,
的图象,且图像关于原点对称,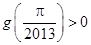 .
.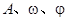 的值;
的值; 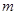 的最小值,并写出
的最小值,并写出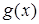 的表达式;
的表达式;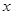 的函数
的函数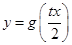 在区间
在区间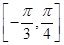 上最小值为
上最小值为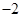 ,求实数
,求实数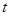 的取值范围.
的取值范围.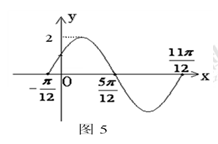

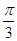 )(ω>0)的单调递增区间为[kπ-
)(ω>0)的单调递增区间为[kπ-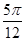 ,kπ+
,kπ+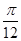 ](k∈Z),单调递减区间为[kπ+
](k∈Z),单调递减区间为[kπ+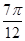 ](k∈Z),则ω的值为________.
](k∈Z),则ω的值为________.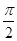 )与g(x)=cos(ωx-
)与g(x)=cos(ωx-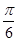 )(ω>0)的图象具有相同的对称中心,则φ=( )
)(ω>0)的图象具有相同的对称中心,则φ=( )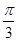
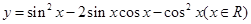 的单调递增区间为 .
的单调递增区间为 .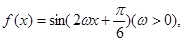 直线
直线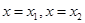 是
是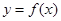 图像的任意两条对称轴,且
图像的任意两条对称轴,且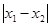 的最小值为
的最小值为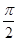 .
.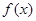 的单调增区间;
的单调增区间;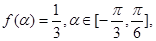 求
求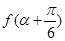 的值;
的值;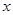 的方程
的方程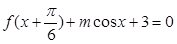 在
在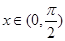 有实数解,求实数
有实数解,求实数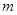 的取值.
的取值.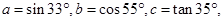 则
则



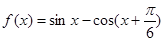 的值域为
的值域为